Question: Can you please help me find the general solution for these problems: The standard form (Ajx + Bly + Ci)dx + (A2x + Bay +
Can you please help me find the general solution for these problems:
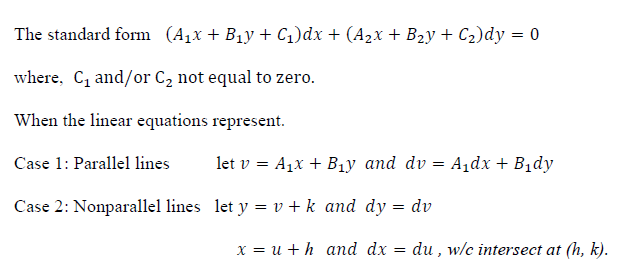

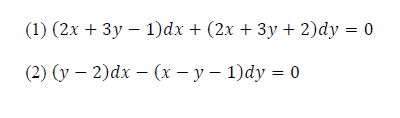
Step by Step Solution
There are 3 Steps involved in it
1 Expert Approved Answer
Step: 1 Unlock


Question Has Been Solved by an Expert!
Get step-by-step solutions from verified subject matter experts
Step: 2 Unlock
Step: 3 Unlock


