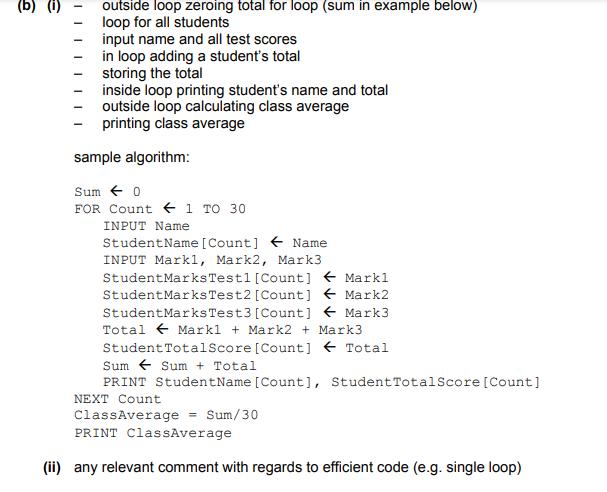
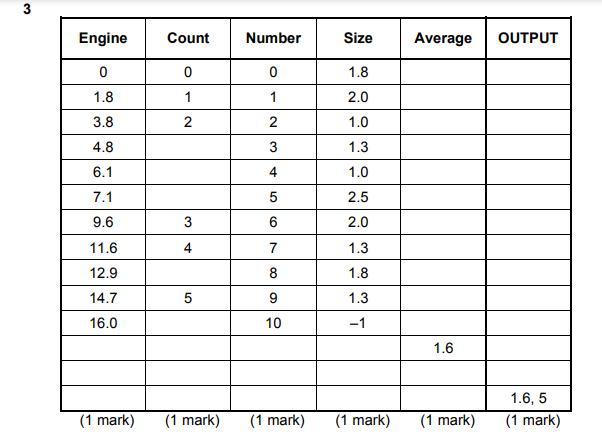
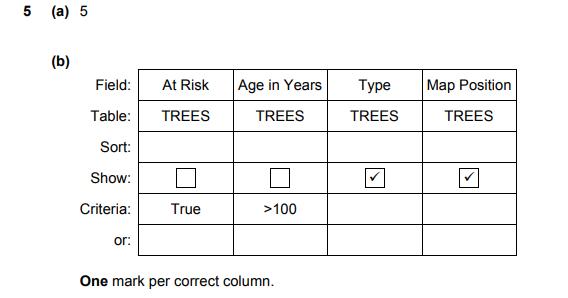
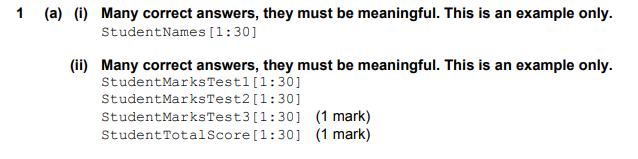CANMNMM

 

 

 

January of this year. (a) Each item will be held in a record. Describe all the data structures that must refer to these records to implement the required functionality. Describe all the fields that the record must have to implement the required functionality, and how each of these fields has to be updated and when. [5 marks] (b) The obvious baseline solution is to re-sort the n items and to take the top k every time the bestseller lists must be produced. Assuming the number of items and the given average rates stay constant, what is its asymptotic worst-case time cost per unit time? [1 mark] (c) Describe three alternative strategies, each better than the baseline, to implement the required functionality. Use the heaps or search trees of your choice, explaining precisely what you would store in each data structure to implement the required functionality. Describe, in each case, how to initialize the data structures, how to update the data structures after each sale, how to recompute the three bestseller lists every s seconds, together with the worst-case asymptotic time cost of each operation as a function of m, n, k, s (cost per unit time for the second and third operations). [6 marks] (d) Recommend the most appropriate strategy for m = 104 , n = 109 , k = 102 , s = 100 , with justification. [2 marks] (e) Repeat for n = 1014 and the other parameters unchanged. [3 marks] (f ) Repeat for m = 10−4 , n = 102 , k = 101 , s = 105 , reasoning about the structural difference between this and the websites of cases (d) and (e). [3 marks] 9 CST0.2021.1.10 9

 

 Algorithms Consider a directed graph in which each edge is labelled by a pair of non-negative costs, for example a distance and a travel time. A path between a pair of nodes is called 'Pareto efficient' (after the economist Vilfredo Pareto) if there is no other path for which both costs are lower. (a) In the graph shown here, find all Pareto efficient paths from s to t, and state their costs. [1 mark] (b) Show that, if v0 → v1 → · · · → vk is a Pareto efficient path from v0 to vk, then v0 → · · · → vk−1 is a Pareto efficient path from v0 to vk−1. [3 marks] (c) Let v0 → · · · vk be a Pareto efficient path from v0 to vk, and let its costs be (ca, cb). Show that there is a Pareto efficient path from v0 to vk with costs (ca, cb) that has ≤ V − 1 edges, where V is the number of vertices in the graph. [3 marks] (d) We are given a start vertex s. Give an algorithm to compute all costs achievable by Pareto efficient paths from s to every other vertex. [6 marks] (e) Prove that your algorithm is correct. [7 marks] 

10 CST0.2021.1.11 10 Algorithms This question is concerned with connected undirected graphs in which each edge has a weight, and with spanning trees in such graphs. (a) Explain what is meant by the translation strategy, and outline briefly the steps of a translation-based proof of correctness. [3 marks] (b) Give an algorithm for finding a maximum spanning tree, that runs in O(E + V log V ) time. Explain why your algorithm's running time is as required. [8 marks] (c) Prove rigorously that your algorithm is correct. [9 marks] [Note: You may refer to algorithms from lecture notes without quoting the code. You may use results from lecture notes without proof, but you must state them clearly

 

 

   

A library defines a generic class Foo in a Java-like language. A user's program declares a class C and subclasses it as class D, creating variables fc and fd of types Foo and Foo respectively. (i) Construct a declaration of Foo along with a program of the above form containing the assignment fc= marks]  indicating any compensating restrictions required for the declaration of Foo or fc to avoid run-time errors. [3 marks] (iii) How do Java arrays of type T[] fit in with your answer to Part (c)(i)? [2 marks] 

2 CST1.2019.7.3 2 Economics, Law and Ethics (a) Describe five different types of auctions. [5 marks] (b) If you were in the business of selling advertisements, what would be an efficient way to price them? [5 marks] (c) How might one political candidate achieve a better price per advertisement than their opponents? [5 marks] (d) What are bidding rings and what might game theory tell us about them? [5 marks] 

3 (TURN OVER) CST1+CST2.2019.7.4 3 Economics, Law and Ethics (a) What do sections 1, 2 and 3 of the Computer Misuse Act 1990 prohibit? [6 marks] (b) Eve is operating a DDoS-for-hire service and has recruited 100,000 CCTV cameras into a botnet. If Mallory pays Eve $2 to take down a gaming teamspeak server for five minutes, what offences, if any, are being committed by Eve and Mallory? [8 marks] (c) How might the Wimbledon case (R v. Lennon 2005 ) apply to this case? [6 marks] 

4 CST1+CST2.2019.7.5 4 Formal Models of Language This question relates to an information source that produces symbols from an alphabet. (a) X is an information source, which produces symbols from the set {a, b, c, d, S} (i) If we assume X produces symbols with equal probability, what is the entropy of X? [1 mark] (ii) In fact, X produces symbols with non-equal probabilities. What do you know about the entropy of X compared to your previous answer? [1 mark] (iii) X produces symbols with probability distribution: p(a) = 0.4, p(b) = 0.2, p(c) = 0.2, p(d) = 0.1, p(S) = 0.1 

Give an expression for the entropy of information source X. [2 marks] (b) The symbol sequence produced by X represents consecutive words of a language, where S indicates whitespace. (i) Describe and provide an equation for the entropy of the language produced by the symbol sequence. [2 marks] (ii) A student observes that when a word in the language contains c it is always followed by b. Explain how this redundancy helps communication over a channel that tends to swap b with d. [2 marks] (c) Define a noisy channel and describe how it could be interpreted with respect to human language communication. [6 marks] (d) Computational Linguists have hypothesised that natural languages have evolved to be both efficient and robust to noise. Do you agree? Justify your answer by referring to information theory and giving appropriate examples. [6 marks] 

5 (TURN OVER) CST1+CST2.2019.7.6 5 Formal Models of Language This question concerns lexical grammars. (a) Tree Adjoining Grammars contain two types of elementary tree. (i) What are these trees called? [1 mark] (ii) If one were building a grammar for English which aspects of language do the two tree types model? [2 marks] (b) Provide a Tree Adjoining Grammar that can parse the string: students enjoy easy exams [5 marks] (c) Show how a parse for this string is constructed. Explain the operations. [5 marks] (d) Provide a Categorial Grammar that can parse the same sentence. [4 marks] (e) When children learn their first language they usually acquire nouns before verbs before modifiers. They also usually produce single word strings before moving on to longer strings. With reference to Tree Adjoining Grammars and/or Categorial Grammars propose some hypotheses for this. Justify your proposals. [3 marks]

    

       

 3 (TURN OVER) CST0.2019.1.4 SECTION B 3 Object-Oriented Programming (a) You are given the following implementation for an element of a list: class Element { int item; Element next; Element(int item, Element next) { super(); this.item = item; this.next = next; } @Override public String toString() { return item + " " + (next == null ? "" : next); } } (i) What does the statement super() mean? [1 mark] (ii) What is the meaning of this in the line this.item = item? [1 mark] (iii) What is the purpose of the annotation @Override? [2 marks] (iv) Rewrite the class to be immutable. You may assume that there are no sub-classes of Element. [2 marks] (b) Use the immutable Element class to provide an implementation of an immutable class FuncList which behaves like an int list in ML. Your class should include a constructor for an empty list and methods head, tail and cons based on the following functions in ML. Ensure that your class behaves appropriately when the list is empty. [6 marks] fun head x::_ = x; fun cons (x,xs) = x::xs; fun tail _::xs = xs; (c) Another developer changes your implementation to a generic class FuncList that can hold values of any type T. (i) This means that FuncList is no longer immutable. Explain why and what could be done to remedy this. [2 marks] (ii) Java prohibits covariance of generic types. Is this restriction necessary in this case? Explain why with an example. [6 marks] 

4 CST0.2019.1.5 4 Object-Oriented Programming (a) What is an object? [2 marks] (b) Give four examples of how object-oriented programming helps with the development of large software projects and explain why each one is helpful. [8 marks] (c) Explain the meaning of the Open-Closed principle. [2 marks] (d) Draw a UML diagram for a design satisfying the Open-Closed principle and explain why it satisfies it. [8 marks] 

5 (TURN OVER) CST0.2019.1.6 SECTION C 5 Numerical Analysis (a) Let f be a single variable real function that has at least one root α, and that admits a Taylor expansion everywhere. (i) Starting from the truncated form of the Taylor expansion of f(x) about xn, derive the recursive expression for the Newton-Raphson (NR) estimate xn of the root at the (n + 1)th step. [1 mark] (ii) Consider the general Taylor expansion of f(α) about xn. Using big O notation for an appropriate Taylor remainder and denoting the NR error at the nth step by en, prove that the NR method has quadratic convergence rate. That is, show that en+1 is proportional to e 2 n plus a bounded remainder. State the required conditions for this to hold, paying attention to the interval spanned during convergence. [6 marks] (iii) Briefly explain two of the known problems of the NR method from an implementation standpoint or otherwise. [2 marks] (b) Let f(x) = x 2 − 1. Suppose we wish to find the positive root of f using the Newton-Raphson (NR) method starting from an initial guess x0 ≥ 1. (i) Show that if x0 ≥ 1 then xn ≥ 1 for all n ≥ 1. [3 marks] (ii) Thus find an upper bound for NR's xn+1 estimate in terms of xn and in turn find an upper bound for xn in terms of x0. [5 marks] (iii) Using the above, estimate the number of NR iterations to obtain the root with accuracy 10−9 for a wild initial guess x0 = 109 . [Hint: You may wish to approximate 103 by 210.] [3 marks] 

6 CST0.2019.1.7 6 Numerical Analysis (a) You are given a system of real equations in matrix form Ax = b where A is non-singular. Give three factorization techniques to solve this system, depending on the shape and structure of A: tall, square, symmetric. For each technique, give the relevant matrix equations to obtain the solution x, and point out the properties of the matrices involved. Highlight one potential problem from an implementation (computer representation) standpoint. [Note: You do not need to detail the factorization steps that give the matrix entries.] [5 marks] (b) We want to estimate travel times between stops in a bus network, using ticketing data. The network is represented as a directed graph, with a vertex for each bus stop, and edges between adjacent stops along a route. For each edge j ∈ {1, . . . , p} let the travel time be dj . The following ticketing data is available: for each trip i ∈ {1, . . . , n}, we know its start time si , its end time fi , and also the list of edges it traverses. The total trip duration is the sum of travel times along its edges. We shall estimate the dj using linear least squares estimation, i.e. solve arg minβ ky − Xβk 2 for a suitable matrix X and vectors β and y. (i) Give an example of ticket data for a trip traversing 5 edges, and write the corresponding equation of its residual. [1 mark] (ii) Give the dimensions and contents of X, β, and y for this problem. State a condition on X that ensures we can solve for β. [3 marks] (iii) Give an example with p = 2 and n = 3 for which it is not possible to estimate the dj . Compute XT X for your example. [2 marks] (c) Let A be an n × n matrix with real entries. (i) We say that A is diagonalisable if there exists an invertible n × n matrix P such that the matrix D = P −1AP is diagonal. Show that if A is diagonalisable and has only one eigenvalue then A is a constant multiple of the identity matrix. [3 marks] (ii) Let A be such that when acting on vectors x = [x1, x2, . . . , xn] T it gives Ax = [x1, x1 −x2, x2 −x3, . . . , xn−1 −xn] T . Write out the contents of A and find its eigenvalues and eigenvectors. Scale the eigenvectors so they have unit length (i.e. so their magnitude is equal to 1). [6 marks] 

7 (TURN OVER) CST0.2019.1.8 SECTION D 7 Algorithms (a) The Post Office of Maldonia issued a new series of stamps, whose denominations in cents are a finite set D ⊂ N{0}, with 1 ∈ D. Given an arbitrary value n ∈ N{0} in cents, the problem is to find a minimum-cardinality multiset of stamps from D whose denominations add up to exactly n. In the context of solving the problem with a bottom-up dynamic programming algorithm. . . (i) Give and clearly explain a formula that expresses the optimal solution in terms of optimal solutions to subproblems. [Note: If your formula gives only a scalar metric (e.g. the number of stamps) rather than the actual solution (e.g. which stamps), please also explain how to obtain the actual optimal solution.] [4 marks] (ii) Draw and explain the data structure your algorithm would use to accumulate the intermediate solutions. [2 marks] (iii) Derive the big-Theta space and time complexity of your algorithm. [1 mark] (b) Repeat (a)(i)-(a)(iii) for the following problem: A car must race from point A to point B along a straight path, starting with a full tank and stopping as few times as possible. A full tank lets the car travel a given distance l. There are n refuelling stations so ≡ A, s1, s2, . . . , sn ≡ B along the way, at given distances d0 = 0, d1, d2, . . . , dn from A. The distance between adjacent stations is always less than l. The problem is to find a minimum-cardinality set of stations where the car ought to refill in order to reach B from A. [7 marks] (c) Which of the two previous problems might be solved more efficiently with a greedy algorithm? Indicate the problem and describe the greedy algorithm. Then give a clear and rigorous proof, with a drawing if it helps clarity, that your greedy algorithm always reaches the optimal solution. Derive the big-Theta time complexity. [6 marks] 

8 CST0.2019.1.9 8 Algorithms (a) Consider a Binary Search Tree. Imagine inserting the keys 0, 1, 2, . . . , n (in that order) into the data structure, assumed initially empty. (i) Draw a picture of the data structure after the insertion of keys up to n = 9 included. [2 marks] (ii) Clearly explain, with a picture if helpful, how the data structure will evolve for arbitrary n, and derive the worst-case time complexity for the whole operation of inserting the n + 1 keys. [2 marks] (b) Repeat (a)(i) and (a)(ii) for a 2-3-4 tree, with some scratch work showing the crucial intermediate stages. [2+2 marks] (c) . . . and for a B-tree with t = 3, again showing the crucial intermediate stages. [2+2 marks] (d) . . . and for a hash table of size 7 that resolves collisions by chaining. [2+2 marks] (e) . . . and for a binary min-heap. [2+2 marks] 

 

 

   

       

1 Digital Electronics (a) Show that (i) (X+Y).(X + Y) = X (ii) (X+Y).(X+Z) = (X + Y).(X+Z).(Y+Z) [5 marks] (b) With the help of the results in Part (a) or otherwise, simplify the following Boolean expression for W in to a product of sums (POS) form having 3 product terms, each having 3 literals W = (A+C+F+G). (A + C + F + G). (A+B+C+D+G) (A+C+E+G).(A+B+G).(B+C+F+G) [10 marks] (c) (i) Using a Karnaugh map, simplify the following Boolean expression for V into a product of sums (POS) form V=A.B.C.D+A.B.C.D+ (A+B+C+D) (ii) Implement the simplified expression for V obtained in Part (c)(i) using only NOR gates. Assume 2 and 4 input gates are available. Also assume complemented input variables are available. [5 marks]