Question: Capa plays either one or two chess games every day, with the number of games that she plays on successive days being a Markov chain

Capa plays either one or two chess games every day, with the number of games that she plays on successive days being a Markov chain with transition probabilities

P1,1 = 0.2, P1,2 = 0.8, P2,1 = 0.4, P2,2 = 0.6.

Capa wins each game with probability p. Suppose she plays two games on Monday.

(a) (2 marks) What is the probability that she wins exactly one game on Tuesday?

(b) (3 marks) What is the expected number of games that she plays on Wednesday?

Below is my own solution. Please verify if they are correct. I'm not too sure about the last question. Thank you!

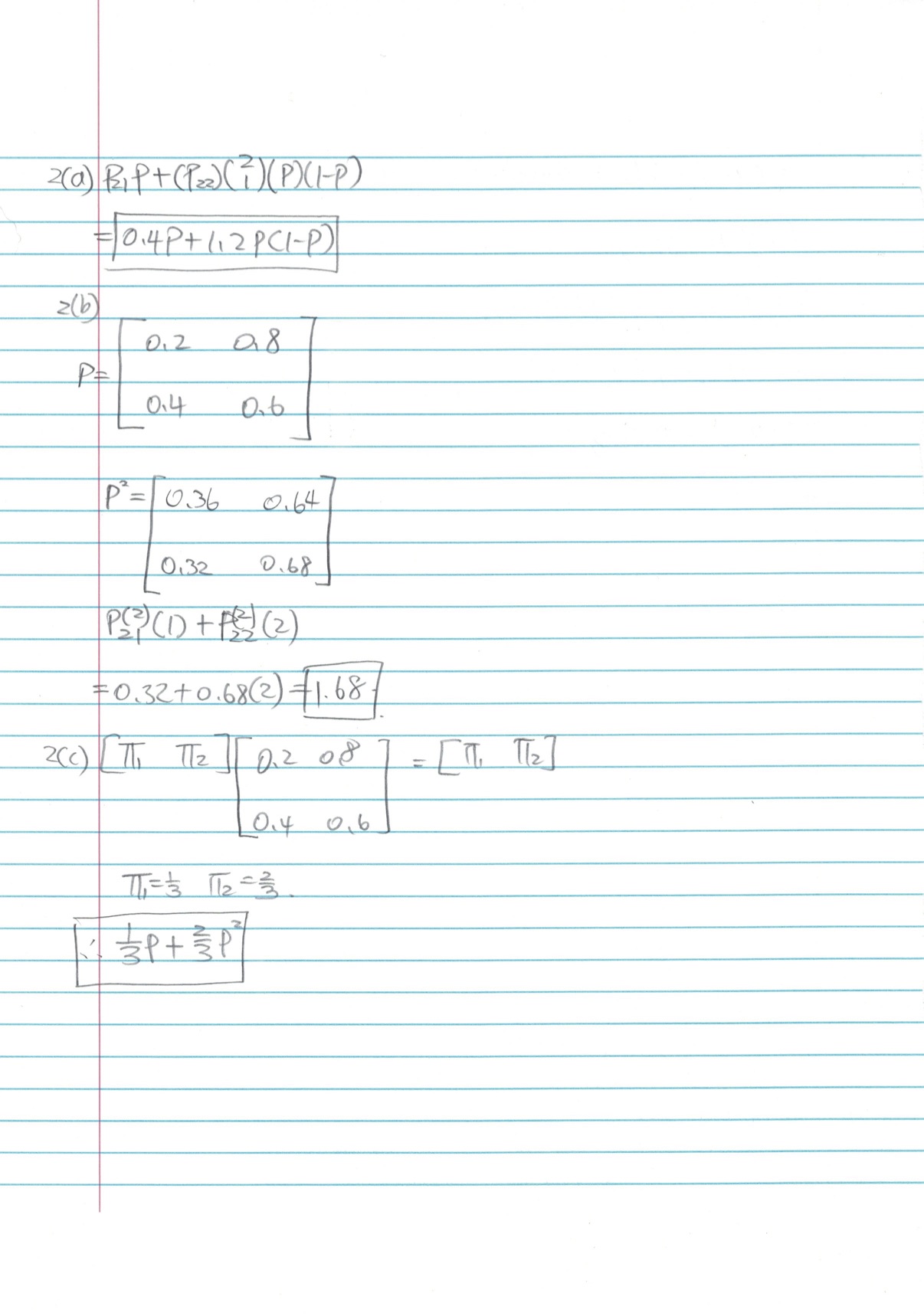
Capa plays either one or two chess games every day, with the

Step by Step Solution

There are 3 Steps involved in it

1 Expert Approved Answer

Step: 1 Unlock blur-text-image

Question Has Been Solved by an Expert!

Get step-by-step solutions from verified subject matter experts

Step: 2 Unlock

Step: 3 Unlock

Students Have Also Explored These Related Mathematics Questions!

Capa plays either one or two chess games every day, with the number of games that she plays on successive days being a Markov chain with transition probabilities P1,1 = .2, P1,2 = .8 P2,1 = .4, P2,2...

38. Capa plays either one or two chess games every day, with the number of games that she plays on successive days being a Markov chain with transition probabilities Capa wins each game with...

Capa plays either one or two chess games every day, with the number of games that she plays on successive days being a Markov chain with transition probabilities Capa wins each game with probability...

Examine the pricing strategies in the gasoline market. Make sure to address the following topics: In the article, (Mixed) Strategy in Oligopoly Pricing: Evidence from Gasoline Price Cycles Before and...

nodes, but at least its bias can be quantified by Markov Chain L. INTRODUCTION analysis and thus can be corrected via appropriate re-weighting The popularity of online social networks (OSNs) in...

Portray in words what transforms you would have to make to your execution to some degree (a) to accomplish this and remark on the benefits and detriments of this thought.You are approached to compose...

Chapter 5 Discrete Markov process Suppose we have a sequence of random variables, {X0 , X1 , . . .} = {Xn } , which is also n=0 called a stochastic process. In this chapter, we study a commonly used...

7. Two chess players, A and B, are going to play 7 games. Each game has three possible outcomes: a win for A (which is a loss for B), a draw (tie), and a loss for A (which is a win for B). A win is...

Briefly describe ASCII and Unicode and draw attention to any relationship between them. [3 marks] (b) Briefly explain what a Reader is in the context of reading characters from data. [3 marks] A...

2017/4/28 Section 6.3 (Part B) [74 points] WebAssign Section 6.3 (Part B) [74 points] (Homework) Current Score : - / 74 Huizhi Liu MA 114, section 601, Spring 2017 Instructor: Lavon Page Due :...

How Words and Symbols Influence Interpersonal Communication Provide two examples of how words and symbols can be used to positively influence interpersonal communication.

Why do states have long-arm jurisdiction statutes?

Due: Tue, Apr 1 5 1 3 0 1 pts Resources Hint Submit Answer Question 1 4 of 1 5

. Chip Hoose is the owner of Hoose Custom Wheels. Chip has just received orders for 1,000 standard wheels and 1,250 deluxe wheels in month 1, 800 standard and 1,500 deluxe for month 2, and 800...