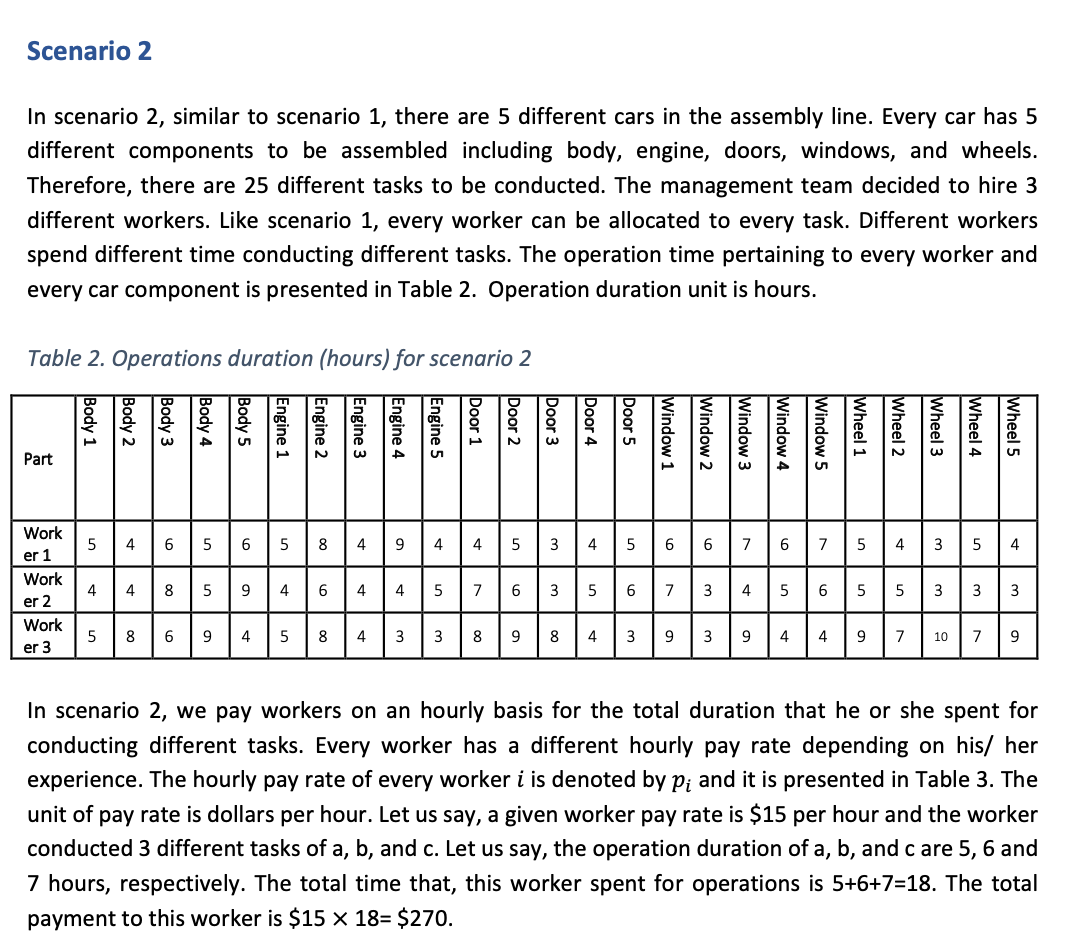
Case description There are four scenarios in this case study. Note that the case description is applicable to scenarios 1, 2 and 3. This case description is not applicable to scenario 4. This case study is about an assembly line of a car manufacturing factory. In this assembly line, different components of a car will be assembled, including body, engine, door, window, and wheels. We use the notation j to represents an assembling task. For example, when j = 1 we refer to task 1, and when j = 25 we refer to task 25. The car components are assembled by the factory workforce. We use the notation i to represents a worker. Every worker, depending on his/her experience and competencies, has a unique processing speed. For example, more experienced workers have a higher speed. At the same time, more experienced workers tend to have a higher salary. The management team of the factory would like to explore the allocation of workers to the assembly line under different scenarios. In this assembly line, there are different types of cars, and every car has unique specifications. Therefore, the processing of different car components needs different processing times. We use operation (i, j) to represent the fact that car component (task j) is assembled (processed) by worker i. We use the notation dij to specify the operation time for processing the task j when it is conducted by worker i. The management team can recruit or hire workers based on the production objective, which can be expressed in terms of minimising production time or maximising production profit or similar measures. In the next section, there are four different scenarios. Every scenario has different numbers of workers, tasks, duration of operation, and other parameters. It is also possible that two different scenarios share a few parameters. Scenario 2 In scenario 2, similar to scenario 1, there are 5 different cars in the assembly line. Every car has 5 different components to be assembled including body, engine, doors, windows, and wheels. Therefore, there are 25 different tasks to be conducted. The management team decided to hire 3 different workers. Like scenario 1, every worker can be allocated to every task. Different workers spend different time conducting different tasks. The operation time pertaining to every worker and every car component is presented in Table 2. Operation duration unit is hours. Table 2. Operations duration (hours) for scenario 2 Body 1 Body 2 Body 3 Body 4 Body 5 Engine 1 Engine 2 Engine 3 Engine 4 Engine 5 Door 1 Door 2 Door 3 Door 4 Door 5 Window 1 Window 2 Window 3 Window 4 Window 5 Wheel 1 Wheel 2 Wheel 3 Wheel 4 Wheel 5 w Part 5 4 6 5 6 5 00 4 9 4 4 5 3 4 5 6 7 6 7 5 4 3 4 Work er 1 Work er 2 Work er 3 4 4. 8 5 9 4 6 4 4. 5 7 6 3 5 6. 7 3 4 5 6 5 5 3 3 3 5 8 9 4 5 8 4 3 3 8 9 8 4 3 9 3 9 4 4 9 7 10 7 9 In scenario 2, we pay workers on an hourly basis for the total duration that he or she spent for conducting different tasks. Every worker has a different hourly pay rate depending on his/her experience. The hourly pay rate of every worker i is denoted by Pi and it is presented in Table 3. The unit of pay rate is dollars per hour. Let us say, a given worker pay rate is $15 per hour and the worker conducted 3 different tasks of a, b, and c. Let us say, the operation duration of a, b, and care 5, 6 and 7 hours, respectively. The total time that, this worker spent for operations is 5+6+7=18. The total payment to this worker is $15 X 18= $270. Table 3. Pay rate of workers for scenario 2 Worker Worker 1 Worker 2 Hourly pay rate $11 $9 $8 Worker 3 The objective of the management team is to minimise production costs. The management team specified the minimum and maximum payment for every worker is $200 and $500, respectively. Other assumptions: No more than one worker can conduct an operation. Once an operation is started the worker keeps conducting the operation until it is finished. All tasks should be processed. . Develop a mathematical model for this problem. Solve the mathematical model with Excel Solver and interpret the results. Case description There are four scenarios in this case study. Note that the case description is applicable to scenarios 1, 2 and 3. This case description is not applicable to scenario 4. This case study is about an assembly line of a car manufacturing factory. In this assembly line, different components of a car will be assembled, including body, engine, door, window, and wheels. We use the notation j to represents an assembling task. For example, when j = 1 we refer to task 1, and when j = 25 we refer to task 25. The car components are assembled by the factory workforce. We use the notation i to represents a worker. Every worker, depending on his/her experience and competencies, has a unique processing speed. For example, more experienced workers have a higher speed. At the same time, more experienced workers tend to have a higher salary. The management team of the factory would like to explore the allocation of workers to the assembly line under different scenarios. In this assembly line, there are different types of cars, and every car has unique specifications. Therefore, the processing of different car components needs different processing times. We use operation (i, j) to represent the fact that car component (task j) is assembled (processed) by worker i. We use the notation dij to specify the operation time for processing the task j when it is conducted by worker i. The management team can recruit or hire workers based on the production objective, which can be expressed in terms of minimising production time or maximising production profit or similar measures. In the next section, there are four different scenarios. Every scenario has different numbers of workers, tasks, duration of operation, and other parameters. It is also possible that two different scenarios share a few parameters. Scenario 2 In scenario 2, similar to scenario 1, there are 5 different cars in the assembly line. Every car has 5 different components to be assembled including body, engine, doors, windows, and wheels. Therefore, there are 25 different tasks to be conducted. The management team decided to hire 3 different workers. Like scenario 1, every worker can be allocated to every task. Different workers spend different time conducting different tasks. The operation time pertaining to every worker and every car component is presented in Table 2. Operation duration unit is hours. Table 2. Operations duration (hours) for scenario 2 Body 1 Body 2 Body 3 Body 4 Body 5 Engine 1 Engine 2 Engine 3 Engine 4 Engine 5 Door 1 Door 2 Door 3 Door 4 Door 5 Window 1 Window 2 Window 3 Window 4 Window 5 Wheel 1 Wheel 2 Wheel 3 Wheel 4 Wheel 5 w Part 5 4 6 5 6 5 00 4 9 4 4 5 3 4 5 6 7 6 7 5 4 3 4 Work er 1 Work er 2 Work er 3 4 4. 8 5 9 4 6 4 4. 5 7 6 3 5 6. 7 3 4 5 6 5 5 3 3 3 5 8 9 4 5 8 4 3 3 8 9 8 4 3 9 3 9 4 4 9 7 10 7 9 In scenario 2, we pay workers on an hourly basis for the total duration that he or she spent for conducting different tasks. Every worker has a different hourly pay rate depending on his/her experience. The hourly pay rate of every worker i is denoted by Pi and it is presented in Table 3. The unit of pay rate is dollars per hour. Let us say, a given worker pay rate is $15 per hour and the worker conducted 3 different tasks of a, b, and c. Let us say, the operation duration of a, b, and care 5, 6 and 7 hours, respectively. The total time that, this worker spent for operations is 5+6+7=18. The total payment to this worker is $15 X 18= $270. Table 3. Pay rate of workers for scenario 2 Worker Worker 1 Worker 2 Hourly pay rate $11 $9 $8 Worker 3 The objective of the management team is to minimise production costs. The management team specified the minimum and maximum payment for every worker is $200 and $500, respectively. Other assumptions: No more than one worker can conduct an operation. Once an operation is started the worker keeps conducting the operation until it is finished. All tasks should be processed. . Develop a mathematical model for this problem. Solve the mathematical model with Excel Solver and interpret the results