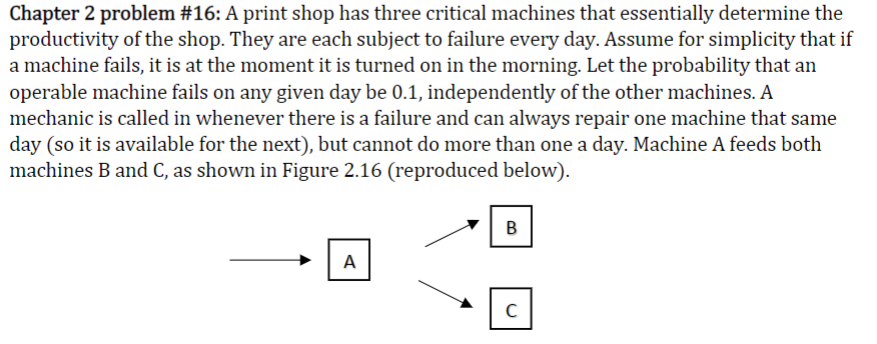
Chapter 2 problem #16: A print shop has three critical machines that essentially determine the productivity of the shop. They are each subject to failure every day. Assume for simplicity that if a machine fails, it is at the moment it is turned on in the morning. Let the probability that an operable machine fails on any given day be 0.1, independently of the other machines. A mechanic is called in whenever there is a failure and can always repair one machine that same day (so it is available for the next), but cannot do more than one a day. Machine A feeds both machines B and C, as shown in Figure 2.16 (reproduced below). B A C Thus, if machine A fails, there is no production that day. Consequently, the policy is always to repair A if it is down. If both B and C are down, and A is up, the policy is to repair B. Of course, units that are down stay down until repaired. Units that are operable today may be down tomorrow, whether or not the shop is able to produce anything. But a unit that is repaired today is certain to operate tomorrow. Develop a Markov chain model to assess the productivity of the shop. Hint: There are eight possible states corresponding to the combinations of up versus down conditions of the three machines. Number these in accordance with the binary numbers. That is, state 0 corresponds to (000), which means all machines are working; state 1 corresponds to 9001), which means A and B are working and C is down; state 2 corresponds to (010), which means A and C are working and B is down; and so on. 16) Referring to problem 16 in Chapter 2 (the print shop problem), use the methods of this chapter to calculate answers to the following questions. a. Classify the states (transient versus recurrent, and so forth). b. What fraction of the time, over the long run, will all of the machines be operable? c. What fraction of the time, over the long run, will there be a machine out of service that the repair person cannot work on because he or she is already occupied in servicing another? d. Explain in detail how to obtain the long-term average production rate of the print shop