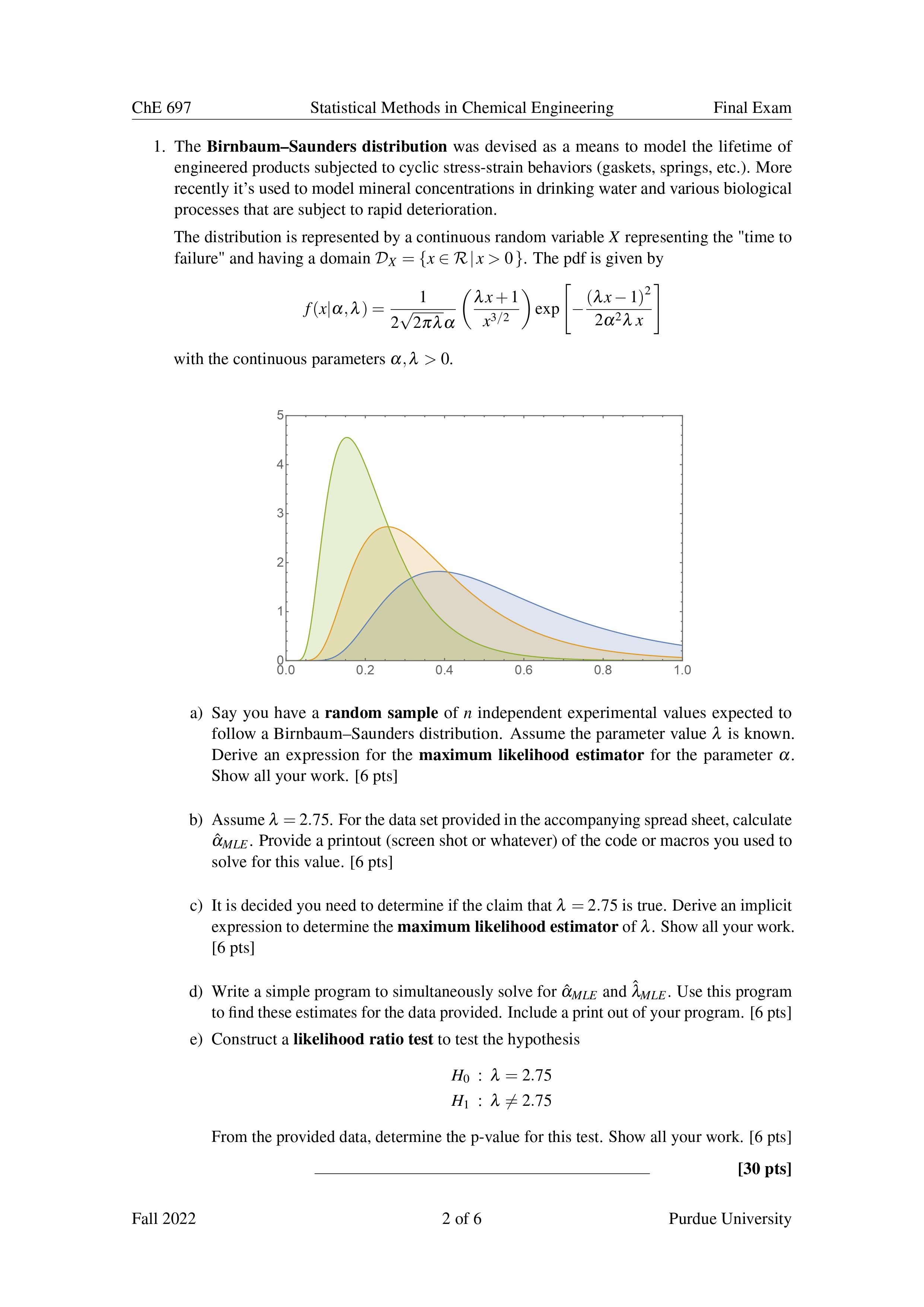
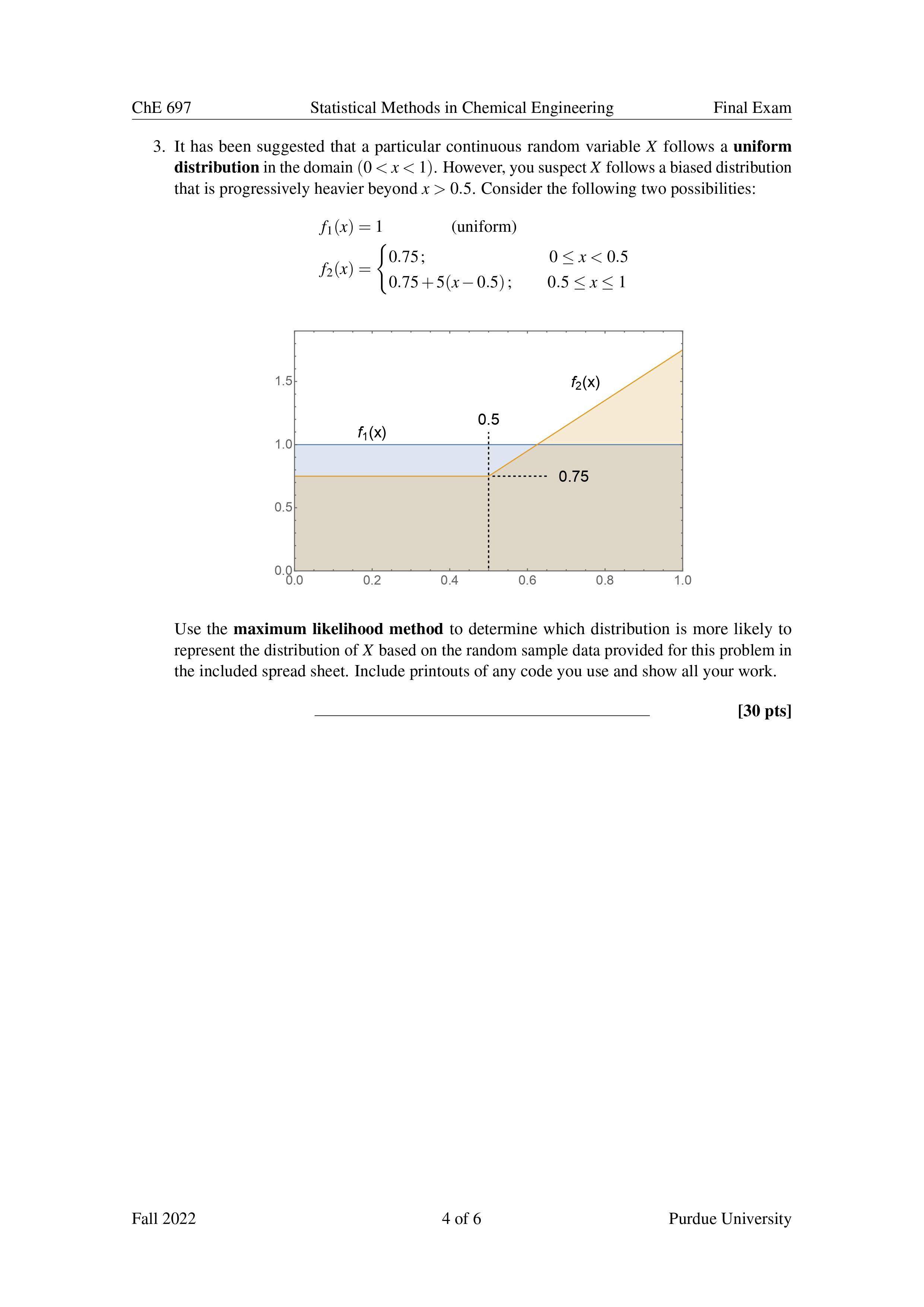
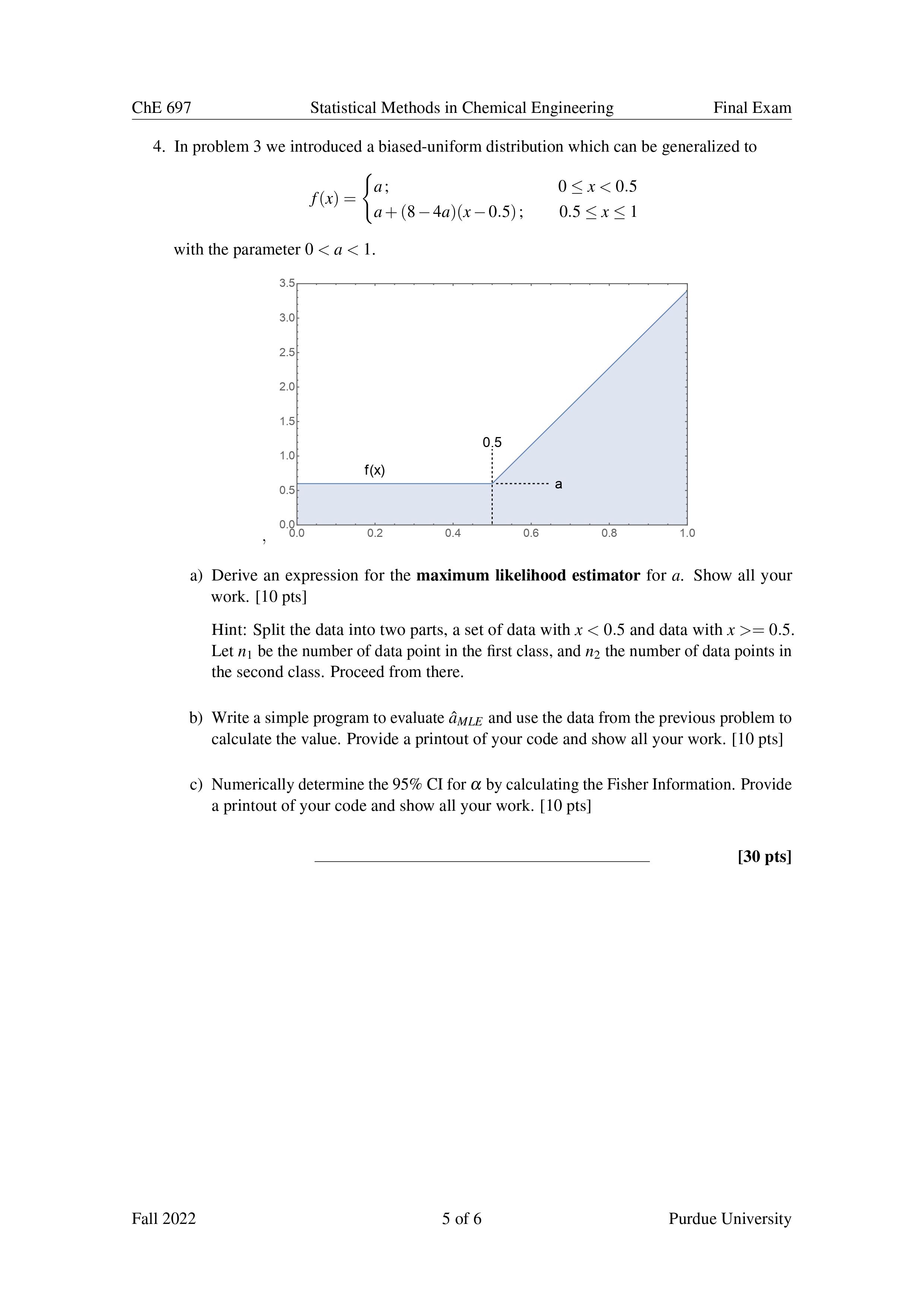
ChE 697 Statistical Methods in Chemical Engineering Final Exam l. The BirnbaumSaunders distribution was devised as a means to model the lifetime of engineered products subjected to cyclic stressstrain behaviors (gaskets, springs, etc.). More recently it's used to model mineral concentrations in drinking water and various biological processes that are subject to rapid deterioration. The distribution is represented by a continuous random variable X representing the "time to failure" and having a domain Dy : {x E Rlx > O}. The pdf is given by .7 2 frxlaar lla(lrxil)exp[ W 1)] 2. 2n- 2062}Lx with the continuous parameters 06,2 > 0. 5 4 3 2 /_ 1. O I I I I 0.0 0.2 0.4 0.6 0.8 1.0 a) Say you have a random sample of n independent experimental values expected to follow a BirnbaumSaunders distribution. Assume the parameter value it is known. Derive an expression for the maximum likelihood estimator for the parameter 05. Show all your work. [6 pts] b) Assume 7L : 2.75. For the data set provided in the accompanying spread sheet, calculate cMLE. Provide a printout (screen shot or whatever) of the code or macros you used to solve for this value. [6 pts] c) It is decided you need to determine if the claim that It : 2.75 is true. Derive an implicit expression to determine the maximum likelihood estimator of A. Show all your work. [6 pts] (1) Write a simple program to simultaneously solve for tMLE and ZMLE. Use this program to nd these estimates for the data provided. Include a print out of your program. [6 pts] e) Construct a likelihood ratio test to test the hypothesis H0 : 2:2.75 From the provided data, determine the p-value for this test. Show all your work. [6 pts] [30 pts] Fall 2022 2 of 6 Purdue University ChE 697 Statistical Methods in Chemical Engineering Final Exam 2. Recall the Birnbaum-Saunders distribution from problem 1. f (yla, 2 ) = - 2v 2 nha In this problem we will derive and test a Bayesian method for estimating the parameter a given that A is known. a) Consider the inverse gamma distribution given by the pdf: ba It (0 |a, b) = [(a) Oatie-b/0 for a, b > 0. Consider the case where a > 1. Show that if we define 0 = a, the inverse gamma distribution is the conjugate prior for the Birnbaum-Saunders distribution in terms of the parameter a. Show all your work. [6 pts] b) Assuming our conjugate prior has hyper-parameter values do and bo, derive the update rules to determine the posterior hyper-parameters an and b, from n data points in a random sample. Show all your work. [8 pts] c) Assume 2 = 3.15. Based on previous studies, the hyper-parameters do = 5 and bo = 2.0 are chosen. From the data provided in problem 1, determine the updated values an and on in the posterior distribution. Plot both the prior and posterior distributions in terms of a-not 0. Provide printouts of any codes you use and show all your work. [8 pts] d) Determine the Bayesian estimate OB and calculate the lower and upper bounds of a 95% Bayesian coverage for a. Include printouts of any code you use and show all your work. [8 pts] [30 pts] Fall 2022 3 of 6 Purdue UniversityChE 697 Statistical Methods in Chemical Engineering Final Exam 3. It has been suggested that a particular continuous random variable X follows a uniform distribution in the domain (0 0.5. Consider the following two possibilities: f1(X) = 1 (uniform) . 0.75; 0 S x 2 0.5. Let m be the number of data point in the rst class, and 112 the number of data points in the second class. Proceed from there. b) Write a simple program to evaluate (EMLE and use the data from the previous problem to calculate the value. Provide a printout of your code and show all your work. [10 pts] c) Numerically determine the 95% CI for 06 by calculating the Fisher Information. Provide a printout of your code and show all your work. [10 pts] [30 pts] Fall 2022 5 of 6 Purdue University ChE 697 Statistical Methods in Chemical Engineering Final Exam 5. Consider the Cauchy distribution given by the probability density function: 1 rows) = W (*w0)- a) Derive expressions for the maximum likelihood estimators. [t and ,3. Show all your work. [7 pts] b) For the data given in the included excel sheet, determine the values 0f ,0 and [3. Attach a hard copy (pdf snap shot) of your code. [8 pts] c) Consider the special case a : 0. Derive an expression for the Fisher information, [(13). Show all your work. [7 pts] (1) Consider now the hypothesis: H0 I [J = 0 H1 I [J $5 0 Determine the likelihood ratio, A, to be used to test this hypothesis. What is the value of A for the above data? Would you reject the null hypothesis for a = 0.05 17 Explain why or why not. Show all your work. [8 pts] [30 pts] Fall 2022 6 of 6 Purdue University