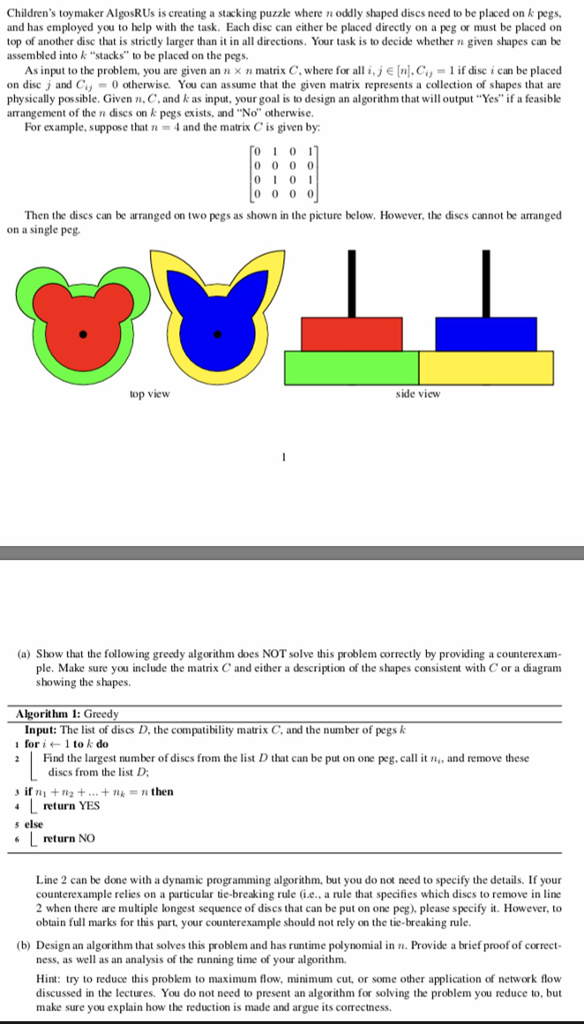
Children's toymaker AlgosRUs is creating a stacking puzzle where n oddly shaped discs need to be placed on k pegs, and has employed you to help with the task. Each disc can either be placed directly on a peg or must be placed on top of another dise that is strictly larger than it in all directions. Your task is to decide whether n given shapes can be assembled into k "stacks" to be placed on the pegs. As input to the problem, you are given an n n matrix C, where for all i, j E [n],C,-1 if disc i can be placed on disc j and C,) = 0 otherwise. You can assume that the given matrix represents a collection of shapes that are physically possible. Given n, C, and k as input, your goal is to design an algorithm that will output "Yes"if a feasibke arrangement of the n discs on k pegs exists, and "No otherwise. For example, suppose that4 and the matrix C is given by 01 0 010 Then the discs can be arranged on two pegs as shown in the picture below. However,the discs cannot be arranged on a single peg. top view side vievw (a) Show that the following greedy algorithm does NOT solve this problem correctly by providing a counterexam- ple. Make sure you include the matrix C and either a description of the shapes consistent with C or a diagram showing the shapes. Algorithm 1: Greedy Input: The list of discs D, the compatibility matrix C, and the number of pegs k |for i l to k do Find the largest number of dises from the list D that can be put on one peg, call it n, and remove these dises from the list D if ni2+.+n then 4 return YES s else 6 return NO Line 2 can be done with a dynamic programming algorithm, but you do not need to specify the details. If your counterexample relies on a particular tie-breaking rule (i.e., a rule that specifies which dises to remove in line 2 when there are multiple longest sequence of discs that can be put on one peg), please secify it. However, to obtain full marks for this part, your counterexample should not rely on the tie-breaking rule (b) Design an algorithm that solves this problem and has runtime polynomial in . Provide a brief proof of correct ness, as well as an analysis of the running time of your algorithm. Hint: try to reduce this problem to maximum flow, minimum cut, or some other application of network flow discussed in the lectures. You do not need to present an algorithm for solving the problem you reduce to, but make sure you explain how the reduction is made and argue its correctness. Children's toymaker AlgosRUs is creating a stacking puzzle where n oddly shaped discs need to be placed on k pegs, and has employed you to help with the task. Each disc can either be placed directly on a peg or must be placed on top of another dise that is strictly larger than it in all directions. Your task is to decide whether n given shapes can be assembled into k "stacks" to be placed on the pegs. As input to the problem, you are given an n n matrix C, where for all i, j E [n],C,-1 if disc i can be placed on disc j and C,) = 0 otherwise. You can assume that the given matrix represents a collection of shapes that are physically possible. Given n, C, and k as input, your goal is to design an algorithm that will output "Yes"if a feasibke arrangement of the n discs on k pegs exists, and "No otherwise. For example, suppose that4 and the matrix C is given by 01 0 010 Then the discs can be arranged on two pegs as shown in the picture below. However,the discs cannot be arranged on a single peg. top view side vievw (a) Show that the following greedy algorithm does NOT solve this problem correctly by providing a counterexam- ple. Make sure you include the matrix C and either a description of the shapes consistent with C or a diagram showing the shapes. Algorithm 1: Greedy Input: The list of discs D, the compatibility matrix C, and the number of pegs k |for i l to k do Find the largest number of dises from the list D that can be put on one peg, call it n, and remove these dises from the list D if ni2+.+n then 4 return YES s else 6 return NO Line 2 can be done with a dynamic programming algorithm, but you do not need to specify the details. If your counterexample relies on a particular tie-breaking rule (i.e., a rule that specifies which dises to remove in line 2 when there are multiple longest sequence of discs that can be put on one peg), please secify it. However, to obtain full marks for this part, your counterexample should not rely on the tie-breaking rule (b) Design an algorithm that solves this problem and has runtime polynomial in . Provide a brief proof of correct ness, as well as an analysis of the running time of your algorithm. Hint: try to reduce this problem to maximum flow, minimum cut, or some other application of network flow discussed in the lectures. You do not need to present an algorithm for solving the problem you reduce to, but make sure you explain how the reduction is made and argue its correctness