Question: Circles and Ellipses: = (t) = a + bsin(t), y (t) = + d cos(t) When a and are zero the circle {or ellipse] is
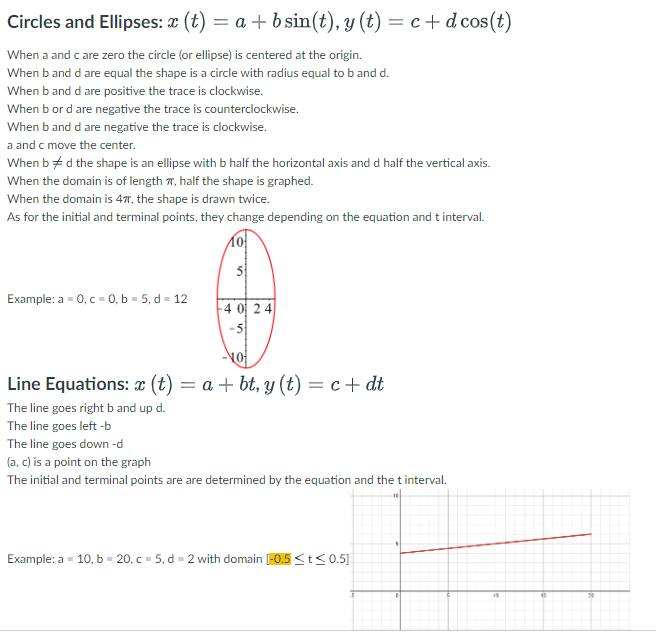

![ellipse] is centered at the origin. When b and d are equal](https://dsd5zvtm8ll6.cloudfront.net/si.experts.images/questions/2024/10/67060e6191789_14567060e61648a0.jpg)
Circles and Ellipses: = (t) = a + bsin(t), y (t) = + d cos(t) When a and are zero the circle {or ellipse] is centered at the origin. When b and d are equal the shape is a circle with radius equal to b and d. When b and d are positive the trace is clockwise. When b or d are negative the trace is counterclockwise. When b and d are negative the trace is dockwise. a and c move the center. When b # d the shape is an ellipse with b half the horizontal axis and d half the vertical axis. When the domain is of length r, half the shape is graphed. When the domain is 447, the shape is drawn twice. As for the initial and terminal points, they change depending on the equation and t interval. Example:a= 0, c= 0. b= 5 d=12 Line Equations: z (t) = a + bt,y () = c + dt The line goes right b and up d. The line goes left -b The line goes down -d (a, ) is a point on the graph The initial and terminal points are are determined by the equation and the t interval. Example:a =10, b= 20, c = 5, d = 2 with domain [BS
Step by Step Solution
There are 3 Steps involved in it

Get step-by-step solutions from verified subject matter experts


