Question: CMSC250 discrete mathematics homework help!! 1. (50 points) We will use Strong Mathematical Induction to show that every positive integer can be written in base

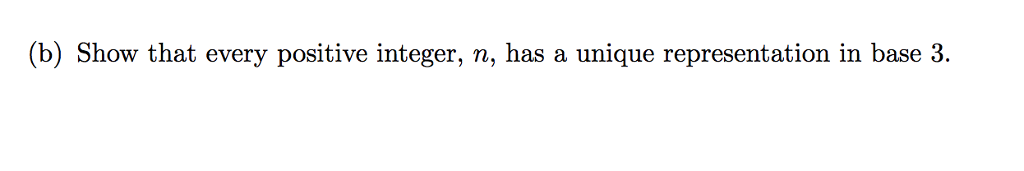
CMSC250 discrete mathematics homework help!! Mathematical Induction to show that every positive integer can be written in

1. (50 points) We will use Strong Mathematical Induction to show that every positive integer can be written in base 3 in a unique way. Your proof should be analogous to the proof in Epp that every positive integer can be written in binary notation in a unique way. (a) Use Strong Mathematical Induction to show that for every positive integer n, there exists a positive integer r, such that where cr-1 1 or 2 and ci-0, 1, or 2 for 0i

Step by Step Solution

There are 3 Steps involved in it

1 Expert Approved Answer

Step: 1 Unlock blur-text-image

Question Has Been Solved by an Expert!

Get step-by-step solutions from verified subject matter experts

Step: 2 Unlock

Step: 3 Unlock

Students Have Also Explored These Related Databases Questions!

CMSC250 discrete mathematics homework help!! 2. (25 points) Assume that you guess that a formula for n. k-1 has the form an2 b2+c, where n 2 1. Use Constructive Mathematical Induction to derive a...

HW 12, MAT 312/AMS 351: SPRING 2017 Problem 1. (1) Set H = {4a + 6b | a, b Z} Z. Show that H is a subgroup of Z. (2) Is H cyclic? Problem 2. Write down all the cyclic subgroups of the following...

3 COLLEGE ALGEBRA - TRIGONOMETRY Business and Finance (MAT115) This course will start with a review of basic algebra (factoring, solving linear equations, and equalities, etc.) and proceed to a study...

In this question you will be asked to reflect on a project you have been involved in or observed, in which a design evolved, or could have evolved, through applying a theory of user behaviour. You...

Let A, B be sets. Define: (a) the Cartesian product (A B) (b) the set of relations R between A and B (c) the identity relation A on the set A [3 marks] Suppose S, T are relations between A and B, and...

Consider the trigonometric series a0 2 + X r=1 (ar cos rx + br sin rx) where a0, a1, a2, . . . and b1, b2, . . . are constants and suppose that f(x) is a periodic function of x with period 2. (a)...

\fCOMPLEX VARIABLES AND APPLICATIONS Eighth Edition James Ward Brown Professor of Mathematics The University of Michigan-Dearborn Ruel V. Churchill Late Professor of Mathematics The University of...

In a Hopfield neural network configured as an associative memory, with all of its weights trained and fixed, what three possible behaviours may occur over time in configuration space as the net...

Math 221 Discrete Mathematics UOPX Make sure all of the are fresh work with proper citation APA format, no used work will be accepted thanks so much. To be substantive, in addition to meeting the...

Can you make any intelligent guesses about why KELLOGG suddenly increased their marketing expenditure?

How important is international trade to the U.S. economy? In terms of volume, does the United States trade more with the industrially advanced economies or with developing economies? What country is...

BE6.2 (LO 2) Restin plc uses the gross method to record sales made on credit. On June 1, 2025, it made sales of 50,000 with terms 3/15, n/45. On June 12, 2025, Restin received full payment for the...

Compared with half a century ago, adoption has become _ _ _ _ _ _ _ _ _ common, but it is more open and acceptabl e , so we probably discuss it _ _ _ _ _ _ _ . fill in the blanks more or much less or...

3. As the HR Manager, you must provide the senior management team with turnover costs for the following high-turnover position. Use websites such as www.talentkeepers.com and www.keepemployees.com,...

LO4 Discuss how flexible work arrangements are linked to worklife balancing efforts.

LO5 Describe job analysis and the stages in the process.