Code a general purpose multiplication procedure for two 32 bit, or two 40 bit, oating point operands, producing either a standard single precision, 32 bit, output or the standard double precision, 64 bit, output.

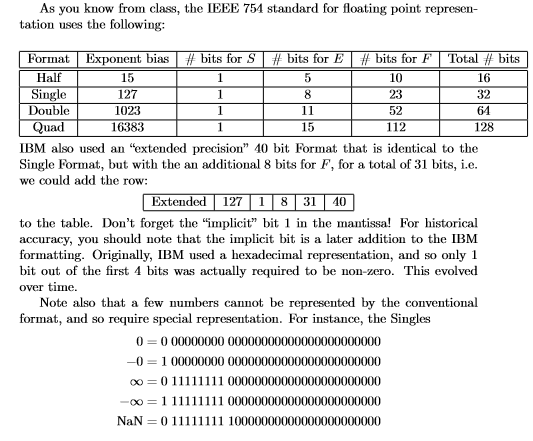
Your code will need to recognize these special cases. You should extend the Single to the other types. You will need to read numbers in both the Single and Extended Formats, and produce multiplication results that are in either Single or Double Formats.

As you know from class, the IEEE 754 standard for floating point represen- tation uses the following: Format | Exponent bias | # bits for S | # bits for E | # bits for F | Total # bits Half Single Double Quad 127 1023 16383 10 23 52 112 16 32 64 128 IBM also used an "extended precision" 40 bit Format that is identical to the Single Format, but with the an additional 8 bits for F, for a total of 31 bits, i.e. we could add the row: Extended 127 18 31 40 to the table. Don't forget the "implicit" bit 1 in the mantissa! For historical accuracy, you should note that the implicit bit is a later addition to the IBM formatting. Originally, IBM used a hexadecimal representation, and so only 1 bit out of the first 4 bits was actually required to be non-zero. This evolved over time. Note also that a few numbers cannot be represented by the conventional format, and so require special representation. For instance, the Singles 0-1 0000000000000000000000000000000 oo0 11111111 00000000000000000000000 -00 1 1 1 1 1 1 1 1 1 00000000000000000000000 NaN- 0 11111111 10000000000000000000000 As you know from class, the IEEE 754 standard for floating point represen- tation uses the following: Format | Exponent bias | # bits for S | # bits for E | # bits for F | Total # bits Half Single Double Quad 127 1023 16383 10 23 52 112 16 32 64 128 IBM also used an "extended precision" 40 bit Format that is identical to the Single Format, but with the an additional 8 bits for F, for a total of 31 bits, i.e. we could add the row: Extended 127 18 31 40 to the table. Don't forget the "implicit" bit 1 in the mantissa! For historical accuracy, you should note that the implicit bit is a later addition to the IBM formatting. Originally, IBM used a hexadecimal representation, and so only 1 bit out of the first 4 bits was actually required to be non-zero. This evolved over time. Note also that a few numbers cannot be represented by the conventional format, and so require special representation. For instance, the Singles 0-1 0000000000000000000000000000000 oo0 11111111 00000000000000000000000 -00 1 1 1 1 1 1 1 1 1 00000000000000000000000 NaN- 0 11111111 10000000000000000000000