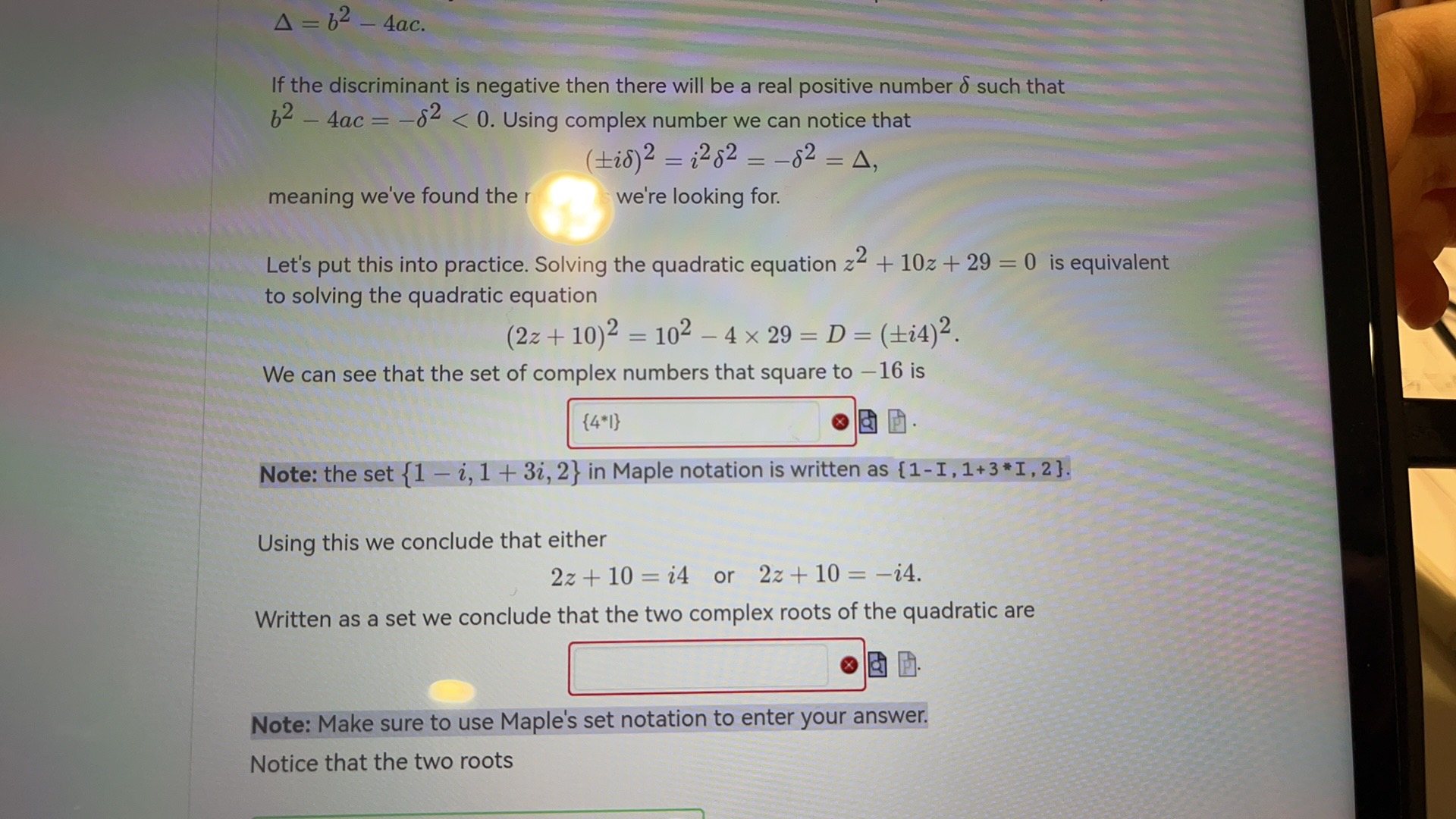
code class$=$"asciimath"$>\backslash$Delta $=$b$^(2)-4$ac If the discriminant is negative then there will be a real positive number $$ such that Using complex number we can notice that $(+-i{)}^2=i^2{}^2=-{}^2=$ meaning we've found the $r$ we're looking for. Let's put this into practice. Solving the quadratic equation $z^2+10z+29=0$ is equivalent to solving the quadratic equation $(2z+10{)}^2={10}^2-429=D=(+-i4{)}^2.$ We can see that the set of complex numbers that square to $-16$ is Note: the set $\{1-i,1+3i,2\}$ in Maple notation is written as $\{1-$I,$1+3*I,2\}.$ Using this we conclude that either $2z+10=i4or2z+10=-i4$ Written as a set we conclude that the two complex roots of the quadratic are Note: Make sure to use Maple's set notation to enter your answer. Notice that the two roots