Code for num_meme_spread plz

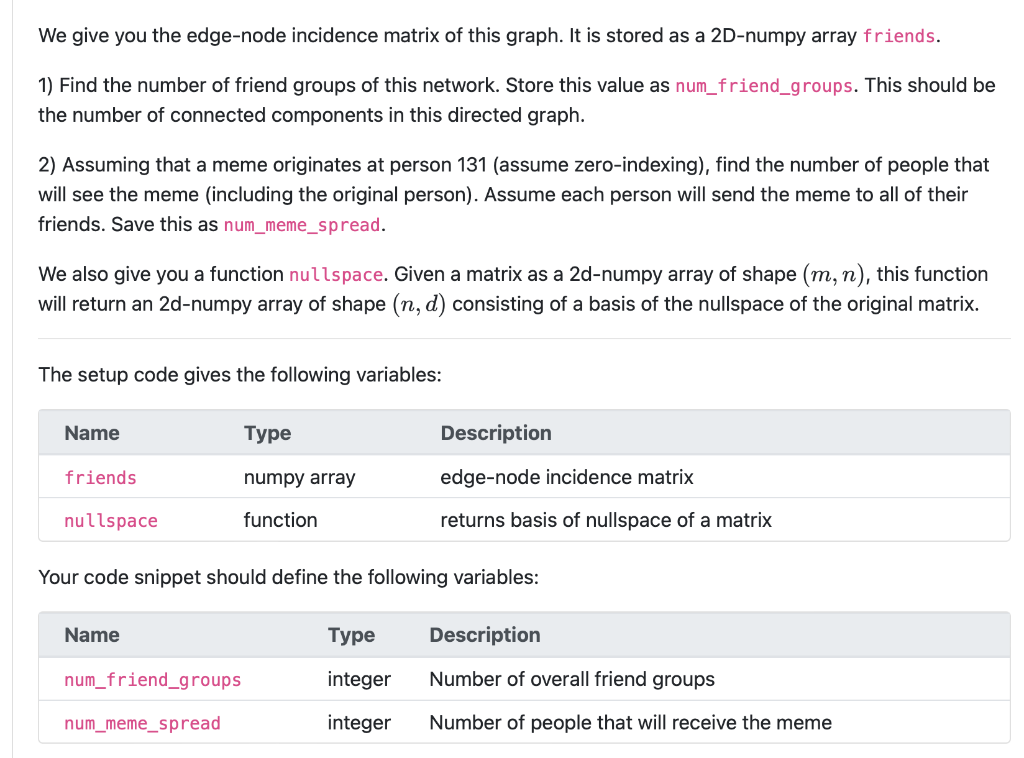
Graphs can be used in mathematics and other fields to represent objects and the connections between them. Here, we will use a directed graph to represent people in a social network and their friend connections with one another. In this directed graph nodes correspond to people. An edge between two nodes indicates frienship between the correspding people. The direction of the edge is chosen at random and carries no further meaning. A friend group is a connected component of this graph. We will use this to model the spread of a meme throughout this theoretical social network. We give you the edge-node incidence matrix of this graph. It is stored as a 2D-numpy array friends. 1) Find the number of friend groups of this network. Store this value as num_friend_groups. This should be the number of connected components in this directed graph. We give you the edge-node incidence matrix of this graph. It is stored as a 2D-numpy array friends. 1) Find the number of friend groups of this network. Store this value as num_friend_groups. This should be the number of connected components in this directed graph. 2) Assuming that a meme originates at person 131 (assume zero-indexing), find the number of people that will see the meme (including the original person). Assume each person will send the meme to all of their friends. Save this as num_meme_spread. We also give you a function nullspace. Given a matrix as a 2 d-numpy array of shape (m,n), this function will return an 2d-numpy array of shape (n,d) consisting of a basis of the nullspace of the original matrix. The setup code gives the following variables: Your code snippet should define the following variables: \( \begin{array}{ll}1 & \text { import numpy as } \mathrm{np} \\ 2 & \text { import numpy.linalg as la } \\ 3 & \\ 4 & \text { num_friend_groups }=\text { nullspace (friends) } . \text { shape }[1] \\ 5 & \text { num_meme_spread }=0\end{array} \) Graphs can be used in mathematics and other fields to represent objects and the connections between them. Here, we will use a directed graph to represent people in a social network and their friend connections with one another. In this directed graph nodes correspond to people. An edge between two nodes indicates frienship between the correspding people. The direction of the edge is chosen at random and carries no further meaning. A friend group is a connected component of this graph. We will use this to model the spread of a meme throughout this theoretical social network. We give you the edge-node incidence matrix of this graph. It is stored as a 2D-numpy array friends. 1) Find the number of friend groups of this network. Store this value as num_friend_groups. This should be the number of connected components in this directed graph. We give you the edge-node incidence matrix of this graph. It is stored as a 2D-numpy array friends. 1) Find the number of friend groups of this network. Store this value as num_friend_groups. This should be the number of connected components in this directed graph. 2) Assuming that a meme originates at person 131 (assume zero-indexing), find the number of people that will see the meme (including the original person). Assume each person will send the meme to all of their friends. Save this as num_meme_spread. We also give you a function nullspace. Given a matrix as a 2 d-numpy array of shape (m,n), this function will return an 2d-numpy array of shape (n,d) consisting of a basis of the nullspace of the original matrix. The setup code gives the following variables: Your code snippet should define the following variables: \( \begin{array}{ll}1 & \text { import numpy as } \mathrm{np} \\ 2 & \text { import numpy.linalg as la } \\ 3 & \\ 4 & \text { num_friend_groups }=\text { nullspace (friends) } . \text { shape }[1] \\ 5 & \text { num_meme_spread }=0\end{array} \)