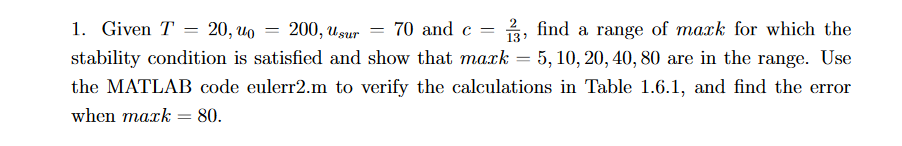
CODE:

function [eulErr] = eulerr2(T,maxk,u0,usur,c) %%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%% % This code compares the discretization errors. % The Euler and improved Euler methods are used. % % Inputs: % maxk = 80; % number of time steps % T = 10.0; % final time % u0 = 200.; % initial temperature % usur = 70.; % surrounding temperature % c = 2./13.; % insulation factor % % Outputs: % eulErr = k x 5 matrix of euler and improved scheme errors at time T % as well as the max errors % % Usage: [eulErr] = eulerr2b(10,5,200,70,2./13) %%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%

for k = 1:6 [ueul,err_eul,uieul,err_im_eul,uexact,time] = eulerr(T,maxk,u0,usur,c); subplot(3,2,k); plot(time,ueul,'b',time,uieul,'g',time,uexact,'r'); legend('Euler','Impr Euler','Exact','Location','NorthEast') xlabel('Time') ylabel('Temperature') title(['Exact & appro solns for maxk = ',num2str(maxk)] ); eulErr(k,1) = maxk; eulErr(k,2) = err_eul(maxk+1); eulErr(k,3) = max(err_eul); eulErr(k,4) = err_im_eul(maxk+1); eulErr(k,5) = max(err_im_eul); maxk = 2*maxk; end end

%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%% % Subroutine: eulererr.m %%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%% function [ueul,err_eul,uieul,err_im_eul,uexact,time] = eulerr(T,maxk,u0,usur,c) %%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%% % This subroutine computes the exact solution, the Euler approx solution, % the improved Euler approx solution, as well as the differences between % analytic and numerical solutions. % % Inputs: % maxk = number of time steps % T = final time % u0 = initial temperature % usur = surrounding temperature % c = insulation factor % % Outputs: % uexact = exact solution % ueul = Euler approx solution % err_eul = Improved Euler approx solution % err_eul = euler scheme error sequence % err_im_eul = Improved Euler scheme error sequence % time = time sequence (needed for plotting) % % Usage: [ueul,err_eul,uieul,err_im_eul,uexact,time] = eulerr(10,5,200,70,2./13) %%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%% dt = T/maxk; time(1) = 0; uexact(1) = u0; ueul(1) = u0; uieul(1) = u0;

for k = 1:maxk time(k+1) = k*dt; % exact solution uexact(k+1) = usur + (u0 - usur)*exp(-c*k*dt); % Euler numerical approximation ueul(k+1) = ueul(k) +dt*c*(usur - ueul(k)); % improved Euler numerical approximation utemp = uieul(k) +dt*c*(usur - uieul(k)); uieul(k+1)= uieul(k) +dt/2*(c*(usur - uieul(k))+c*(usur - utemp)); err_eul(k+1) = abs(ueul(k+1) - uexact(k+1)); err_im_eul(k+1) = abs(uieul(k+1) - uexact(k+1)); end end

180 160 140 120 100 80 50 knax maxk-40 mask 20 mack 5 40 20 0 10 20 30 50 Figure 1.6.1: Euler Approximations Time Steps Euler ErrorImproved Euler Error 10 20 40 7.2378 3.4536 1.6883 0.8349 0.8655 0.1908 0.0449 0.0109 180 160 140 120 100 80 50 knax maxk-40 mask 20 mack 5 40 20 0 10 20 30 50 Figure 1.6.1: Euler Approximations Time Steps Euler ErrorImproved Euler Error 10 20 40 7.2378 3.4536 1.6883 0.8349 0.8655 0.1908 0.0449 0.0109