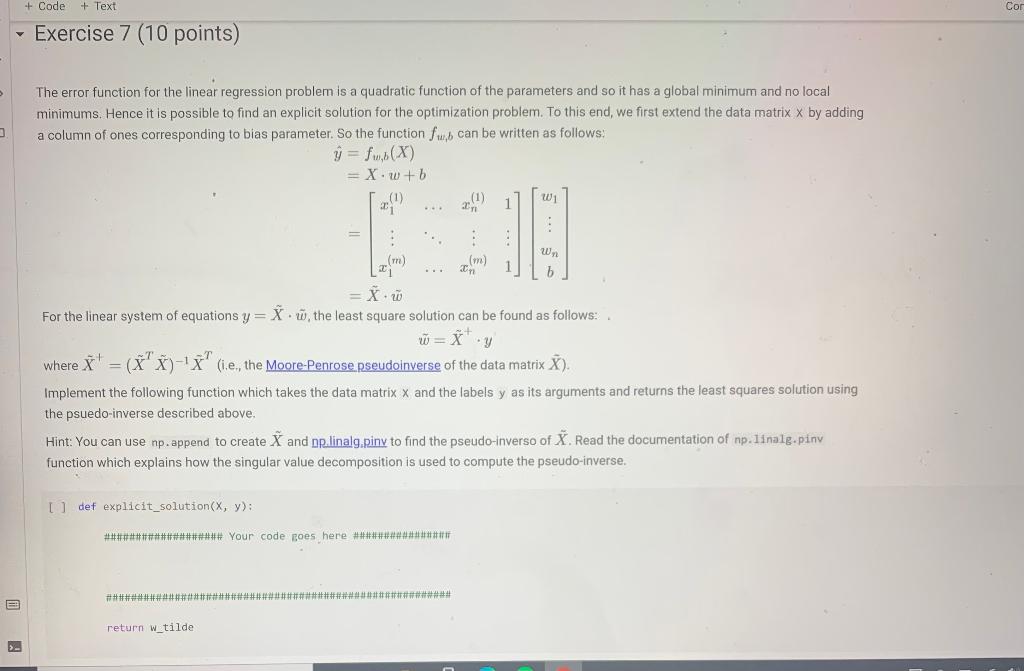
+ Code + Text CO Exercise 7 (10 points) The error function for the linear regression problem is a quadratic function of the parameters and so it has a global minimum and no local minimums. Hence it is possible to find an explicit solution for the optimization problem. To this end, we first extend the data matrix x by adding a column of ones corresponding to bias parameter. So the function fub can be written as follows: fu, (X) =Xw+b 2 : m (m) 21 Un = X For the linear system of equations y=X, the least square solution can be found as follows: TA u = x+ where it (x - 18 (i.e, the Moore Penrose pseudoinverse of the data matrix X). Implement the following function which takes the data matrix X and the labels y as its arguments and returns the least squares solution using the psuedo-inverse described above. Hint: You can use np.append to create X and oplinalg.piny to find the pseudo-inverso of X. Read the documentation of np. linalg-piny function which explains how the singular value decomposition is used to compute the pseudo-inverse. 0 def explicit_solution(x, y): ############## Your code poes here ### return w_tilde + Code + Text CO Exercise 7 (10 points) The error function for the linear regression problem is a quadratic function of the parameters and so it has a global minimum and no local minimums. Hence it is possible to find an explicit solution for the optimization problem. To this end, we first extend the data matrix x by adding a column of ones corresponding to bias parameter. So the function fub can be written as follows: fu, (X) =Xw+b 2 : m (m) 21 Un = X For the linear system of equations y=X, the least square solution can be found as follows: TA u = x+ where it (x - 18 (i.e, the Moore Penrose pseudoinverse of the data matrix X). Implement the following function which takes the data matrix X and the labels y as its arguments and returns the least squares solution using the psuedo-inverse described above. Hint: You can use np.append to create X and oplinalg.piny to find the pseudo-inverso of X. Read the documentation of np. linalg-piny function which explains how the singular value decomposition is used to compute the pseudo-inverse. 0 def explicit_solution(x, y): ############## Your code poes here ### return w_tilde