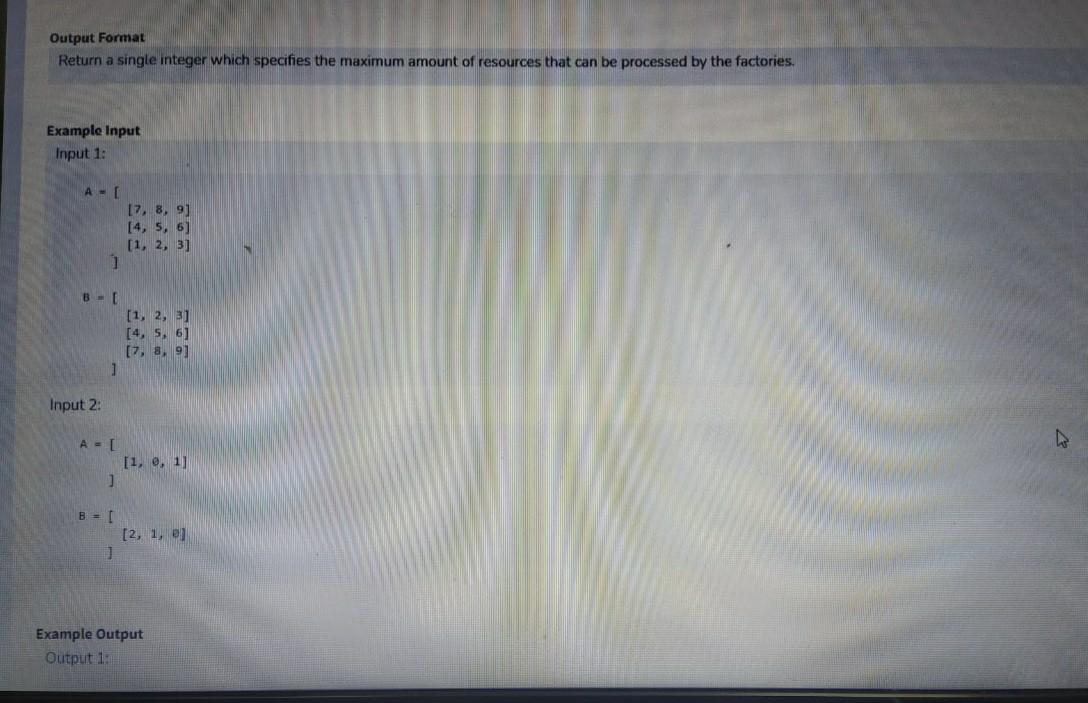
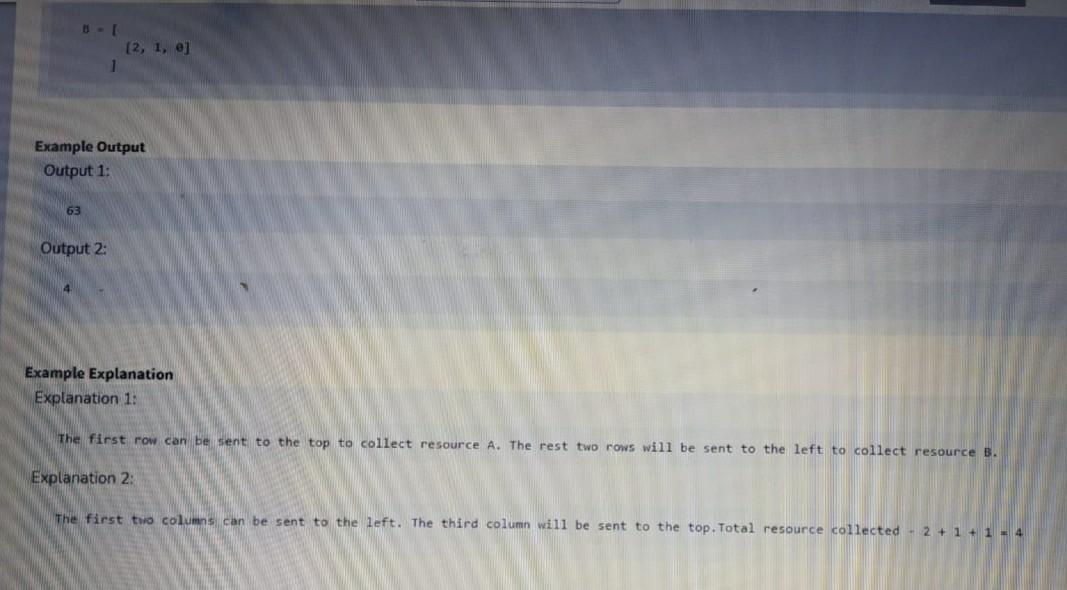
Collect Resources Problem Description There is a rectangular field with two types of resources viz, resource A and resource B. At each cell in the field, both of the resources can be present. The factories which can collect resource A and B. If resource A is collected in a factory then resource B is lost and vice versa. Now, these two factories are loc to each other i.e the factory collecting resource A is at the top (north) of the rectangular field and the factory collecting resource B is to the left (West) field. The resources have to be brought to the factory on a straight path without taking any turns. This implies that if there is any south-north conveyor the cell north of it contains an east-west conveyor belt, then all resources transported on the south-north conveyor belt will be lost. You have to design a conveyor belt system that maximizes the total amount of minerals mined, ie the sum of the amount of resource A transported to th of the amount of resource B transported to the left. You are given a 2-D matrix A and B of the same size denoting the amount of resource of the correspc cell Since the answer can be large, return it modulo 10 +7. Problem Constraints 1 > XA, vector vector int> >&B) { 2