Complete all 10 questions please mark the final answer clearly and step by step!

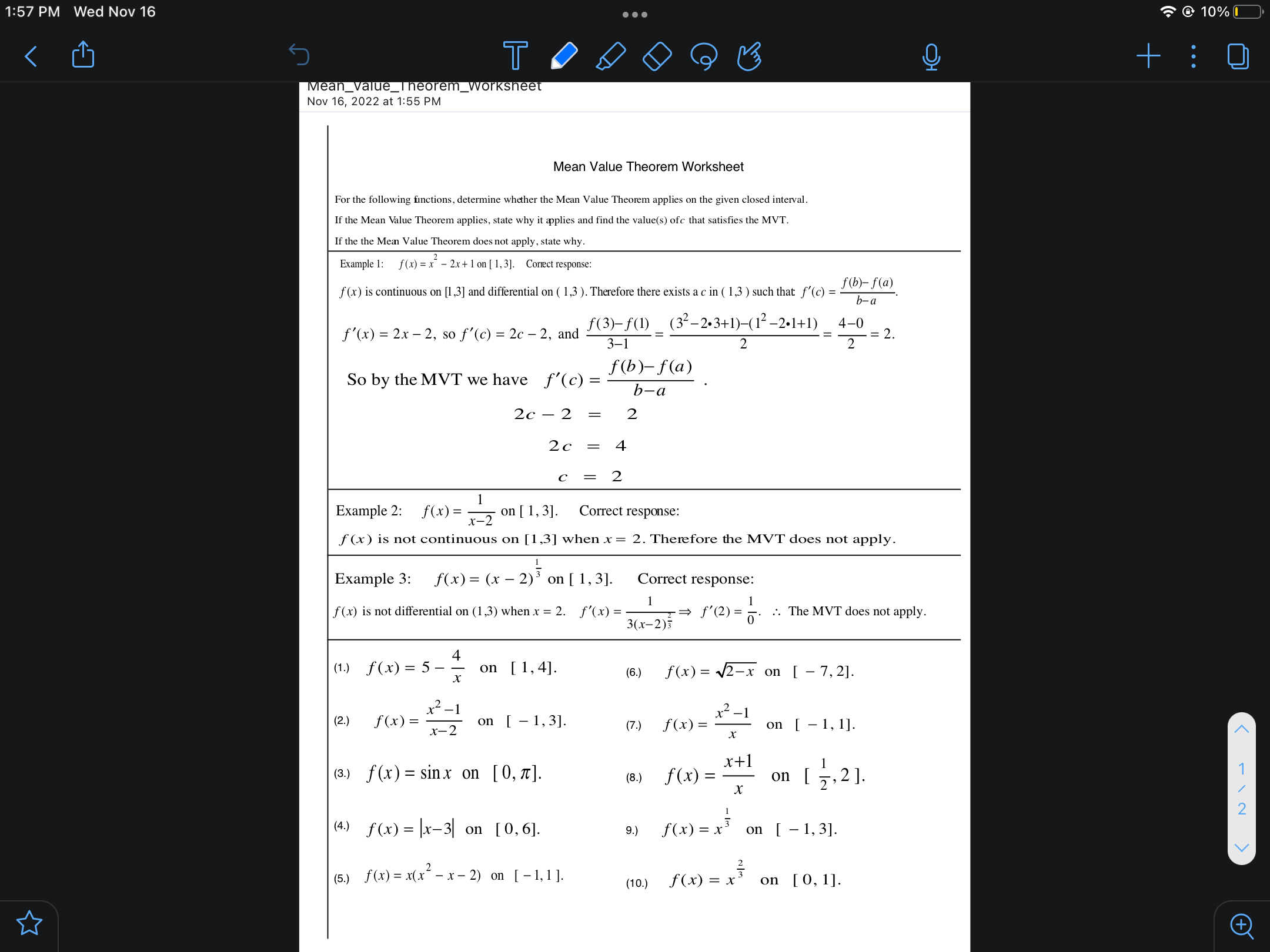
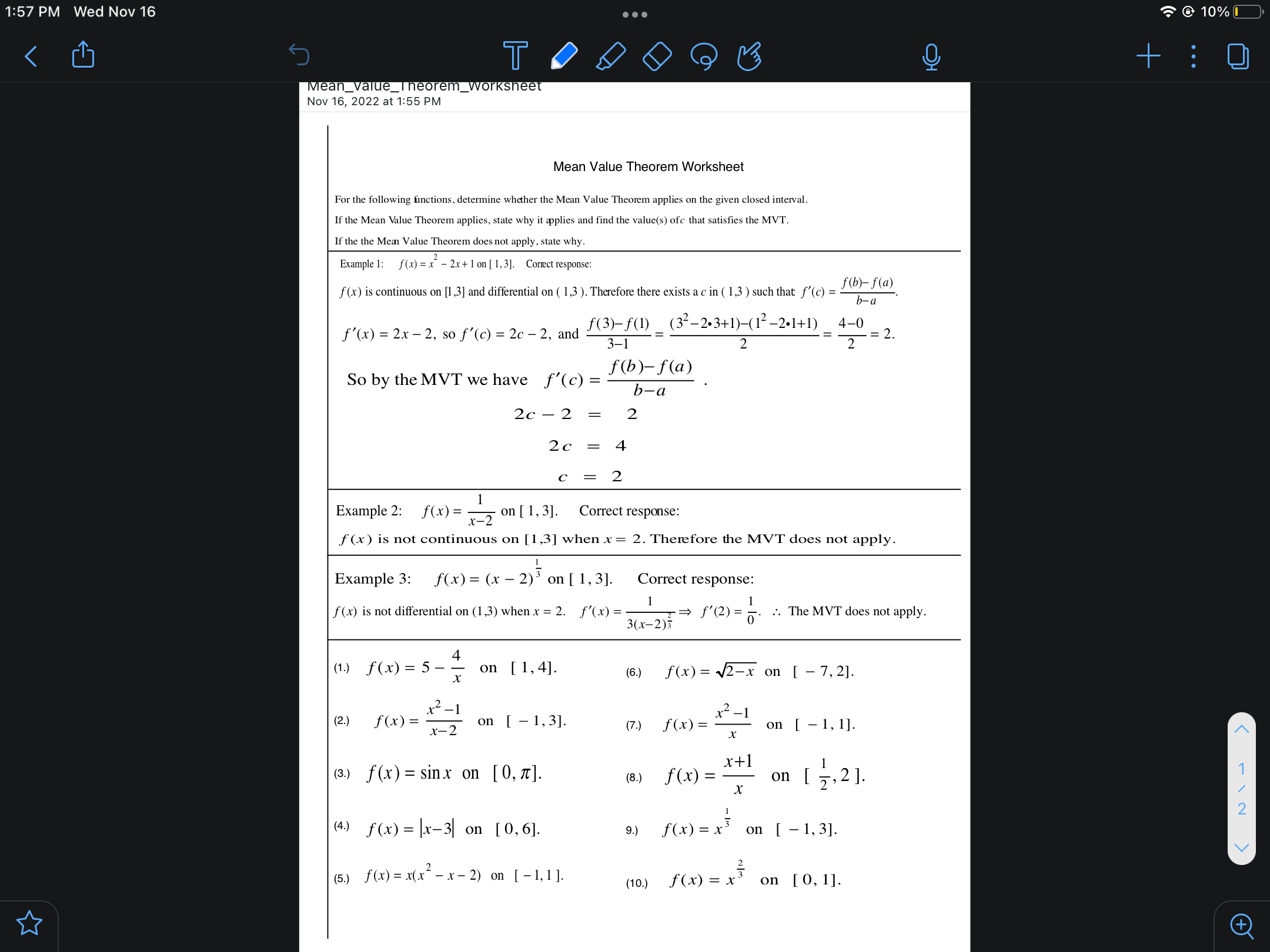
1:57 PM Wed Nov 16 . . @ 10% TO O +: 0 Mean_Value_Theorem_Worksheet Nov 16, 2022 at 1:55 PM Mean Value Theorem Worksheet For the following finctions, determine whether the Mean Value Theorem applies on the given closed interval. If the Mean Value Theorem applies, state why it applies and find the value(s) ofc that satisfies the MVT. If the the Mean Value Theorem does not apply, state why. Example 1: f(x) = x - 2x + 1 on [ 1, 3]. Correct response: f(x) is continuous on [1,3] and differential on ( 1,3 ). Therefore there exists a c in ( 1,3 ) such that f'(c) = - = f(b)-f(a) b-a f'(x) = 2x - 2, so f'(c) = 2c - 2, and f(3)-f(1) _(3--2.3+1)-(12-2.1+1) 4-0 3-1 2 2 = 2. So by the MVT we have f'(c) = f(b)-f(a) b-a 20- 2 = 2 2c 4 C 2 Example 2: f(x) = 1 x-2 on [ 1, 3]. Correct response: f (x) is not continuous on [1,3] when x = 2. Therefore the MVT does not apply. Example 3: f(x) = (x - 2)3 on [ 1, 3]. Correct response : f (x) is not differential on (1,3) when x = 2. f'(x) = - 3(x-2)3 I = f' ( 2 ) = 0 .. The MVT does not apply. ( 1 .) f ( x ) = 5 - - on [ 1, 4]. (6.) f (x) = v2-x on [ - 7, 2]. ( 2 . ) f ( x ) = - x 2 - 1 x - 2 on [ - 1, 3]. (7.) f (x ) = _ *2 -1 x on [ - 1, 1]. (3.) f (x) = sinx on [0, x]. x+1 (8.) f(x ) = on [ 7, 2 ]. X N I - (4.) f (x) = |x-3 on [0, 6]. 9.) f (x) = x' on [ - 1, 3].