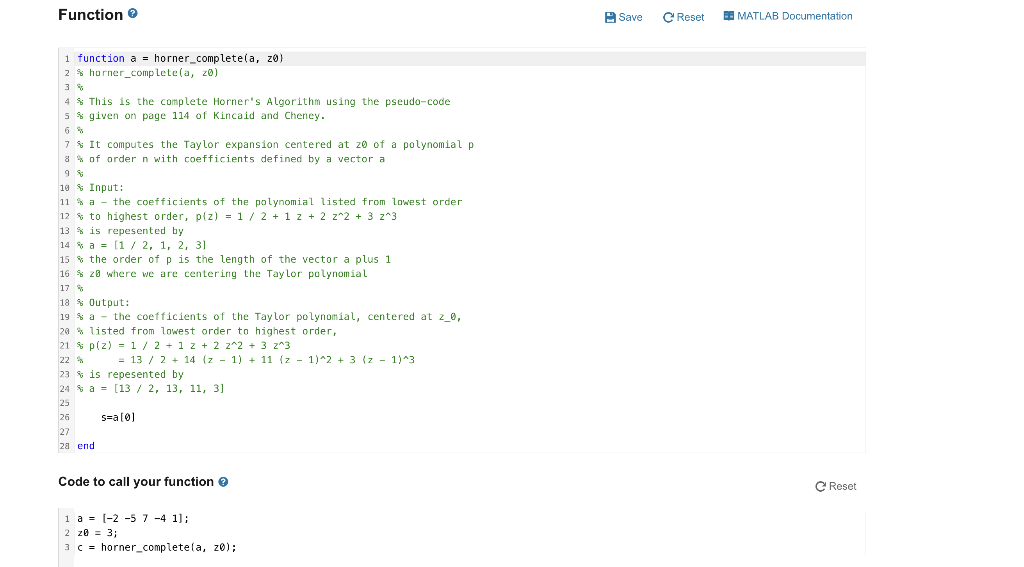
complete Horner's algorithm My Solutic The Taylor polynomial centered at z0 of a polynomial p can be computed using Horner's method. In essence, you keep dividing the polynomial by the term ( zz0) and keep track of the coefficient b1. For an example of this, see page 114 from the textbook: z44z3+7z25z2=(z3)4+8(z3)3+25(z3)2+37(z3)+19. Your job is to implement the complete Horner's algorithm from the pseudo code found in the textbook. input n,(ai:0in),z0 for k=0 to n1 do forj=n1tokstep1do ajaj+z0aj+1 end do end do output (ai:0in) Your function should accept the following inputs: a - vector containing the coefficients of the polynmial of degree n, of size 1 by (n+1), where the coefficients of the polynomial are listed from lowest order to highest order. For example, p(z)=1/2+z+2z2+3z3 is represented by a=[1/2,1,2,3] z0 - where the Taylor polynomial will be centered. Your function should return the following output: a - vector containing the coefficients of the Taylor polynomial of degree n centered at z0, where the coefficients of the polynomial are listed from lowest order to highest order. For example, z44z3+7z25z2=(z3)4+8(z3)3+25(z3)2+37(z3)+19,z0=3 is represented by a =[19,37,25,8,1] Code to call your function