Complete the c program

#include #include

#define EPSILON 1e-6

/* we define the following structure types for representing matrix and vector */ /* functions may pass structures as parameters and also return a structure */ typedef struct { double m[9][9]; int dim; } MatrixType;

typedef struct { double v[9]; int dim; } VectorType;

/* given example */ /* * return a patterned new n x n matrix */ MatrixType initPatternMatrixNxN(int n) { MatrixType newMatrix = {{0}, n}; int row, col; for (row = 0; row

return newMatrix; }

/* return a new copy of a source matrix */ MatrixType copyMatrixNxN(MatrixType src) { MatrixType newMatrix = {{0}, src.dim}; int row, col; for (row = 0; row

return newMatrix; }

/* print a matrix */ void printMatrixNxN(MatrixType mat) { int col; printf("/"); for (col = 0; col

/* print n x n matrix mat.m content here */

printf("\\"); for (col = 0; col

/* construct and return a minor matrix of dimensions (N-1)x(N-1) */ /* i.e., remove a row and remove a column from the source matrix M */ MatrixType extractMinorMatrixNxN(MatrixType M, int removeMrow, int removeMcol) { MatrixType result; result.dim = M.dim - 1; int Rrow, Rcol; int Mrow, Mcol;

return result; }

/* RECURSIVELY, find and return determinant of a matrix */ double detMatrixNxN(MatrixType M) { // base termination case if (M.dim == 1) return M.m[0][0];

double det = 0; int row;

// cofactor expansion recursively // expand col 0 always for (row = 0; row

/* construct and return a new matrix of dimensions NxN */ /* by replacing a column from vector V */ MatrixType replaceOneColumnInMatrixNxN(MatrixType M, VectorType V, int replaceMcol) { MatrixType result; return result; }

/* solve a system of linear equations using Cramer's rule */ VectorType solveEquation(MatrixType A, VectorType b) { VectorType result; return result; }

/* read a system of equation from the user */ /* return number of equations read, i.e., dimension of matrix, and symbol count */ int readFromUserEquationNxN(double coeff[9][9], char symbols[9], double constants[9]) { int N; int row, col;

printf("Number of equations [1-9]: "); scanf("%d", &N);

for (row = 0; row

scanf("=%lf", &constants[row]); }

return N; }

void printEquationNxN(double coeff[9][9], char symbols[9], double constants[9], int N) {

}

int main() { printf("Math Tool Box "); printf("/\\/\\/\\/\\/\\/\\/ ");

{ printf("Phase 3A ");

/* in general, we can handle NxN matrix with max N = 9 */

// sample code for your reference MatrixType Y; Y = initPatternMatrixNxN(5);

MatrixType Z; Z = copyMatrixNxN(Y);

VectorType W; W.dim = Z.dim; W.v[0] = 1.0; W.v[1] = -0.9; char unknowns[9];

printEquationNxN(Z.m, unknowns, W.v, Z.dim);

// your work here

// if determinant of the matrix is less than 0.000001 printf("There is no solution! ");

}

return 0; }

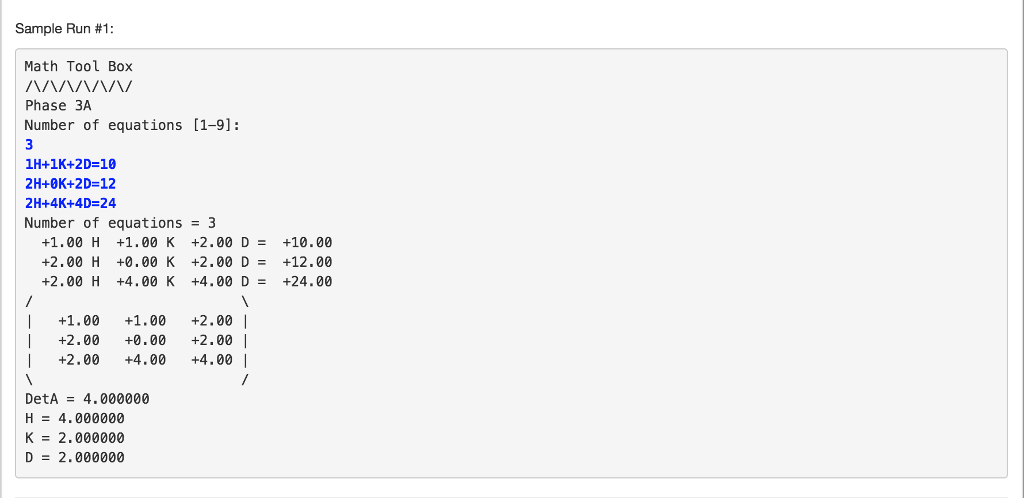
Sample Run #1 Math Tool Box wVVV Phase 3A Number of equations [1-9]: 1H+1K+2D-10 2H+9Kt2D=12 2H+4K+4D 24 Number of equations = 3 +1.00 H +1.00 K +2.00 D= +10.00 +2.00 H +0.00 K +2.00 D = +12.00 +2.00 H +4.00 K +4.00 D= +24.00 | +1.00 +1.00 +2.00 | +2.00 +0.00 +2.00 | | +2.00 +4.00 +4.00 | DetA = 4.000000 H = 4.000000 K = 2.000000 D = 2.000000 Sample Run #1 Math Tool Box wVVV Phase 3A Number of equations [1-9]: 1H+1K+2D-10 2H+9Kt2D=12 2H+4K+4D 24 Number of equations = 3 +1.00 H +1.00 K +2.00 D= +10.00 +2.00 H +0.00 K +2.00 D = +12.00 +2.00 H +4.00 K +4.00 D= +24.00 | +1.00 +1.00 +2.00 | +2.00 +0.00 +2.00 | | +2.00 +4.00 +4.00 | DetA = 4.000000 H = 4.000000 K = 2.000000 D = 2.000000