Complete the following four hypotheses, using = 0.05 for each.

• 1. Mean sales per week exceed 40.5 per salesperson
• 2. Proportion receiving online training is less than 54%
• 3Mean calls made among those with no training is at least 140
• 4. The mean time per call is 14.7 minutes
• Using the same data set from part A, perform the hypothesis test for each speculation in order to see if there is evidence to support the manager's belief.
• Compute 99% confidence intervals for the variables used in each hypothesis test and interpret these intervals.
• Provide a report about the results, distilling down the results in a way that would be understandable to someone who does not know statistics. Clear explanations and interpretations are critical.

Part B: Hypothesis Testing and Confidence Interval

We shall look at four hypotheses of the manager for the set data and evaluate the information with a confidence interval of 99 %.

Hypothesis Test #1

Claim: Mean sales per week exceed 40.5 per salesperson

Step 1: H₀a >40.5 (claim)

Step 2: Put information into the spreadsheet

Step 3: This is a right-tailedthe p-valueright-tailedthe p-value test, meaning that the error is on the right side of the distribution

Step 4: Determine p value. The right-sided p-value is 0.000028, which is less than alpha, our significance level.

Level of Significance	0.05
Mean under H0	40.5
n	100
Sample Mean	43.63
StDev	7.44
Use t or z?	t

Step 3: This is a right tailed test, meaning that the error is on the right side of the distribution

Step 4: Determine p value. The right-sided p-value is 0.000028, which is less than alpha, our significance level.

SE	0.744000
Test statistic	4.206989
Left-sided p-value	0.999972
Right-sided p-value	0.000028
Two-Sided p-value	0.000026

Step 5: We reject H0 because p 0 because p a.BecauseH_ais the claim, we take the manager's claim that mean sales per week exceed 40.5 per salesperson.

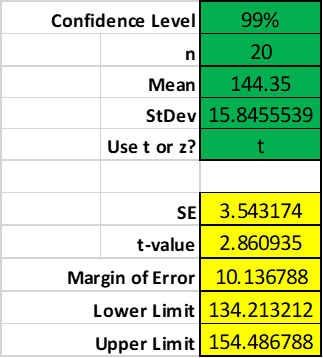
Confidence interval for hypothesis #1:

Now we determine if outhe 99% confidence interval reflects our result

	Confidence Level	99%
	n	100
	Mean	43.63
	StDev	7.44
	Use t or z?	t
	SE	0.744000
	t-value	2.626405
	Margin of Error	1.954046
	Lower Limit	41.675954
	Upper Limit	45.584046

According to our calculation, we are 99% confident that the actual mean sales per salesperson are between 41.68 and 45.58. Therefore, not only are our mean sales > 40.5 per salesperson, but there ia s 99% chance that they are actually between 42 and 46.

Hypothesis Test #2

Claim: Proportion of salesperson receiving online training is less than 54% out of all salesperson.

Step 1: H₀> =54%; H_a

Step 2: Put information into the proportion side spreadsheet

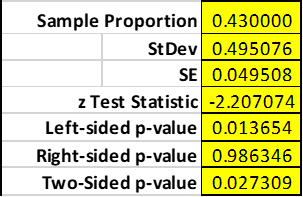
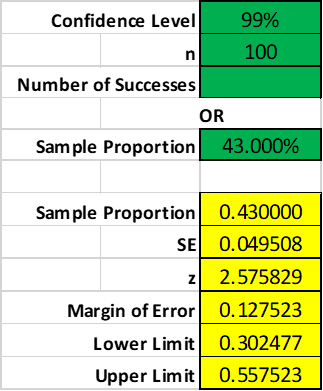
Level of Significance Proportion under Ho n Numbe r of Successes 0R Sample Proportion _ 0.430000 0.495076 0.049508 -2.207074 0.013654 0.986346 0.027309