Question: Complete the square and find the indefinite integral. (Use C for the constant of integration. ) x 2 dx 2x - x2Find the indefinite integral

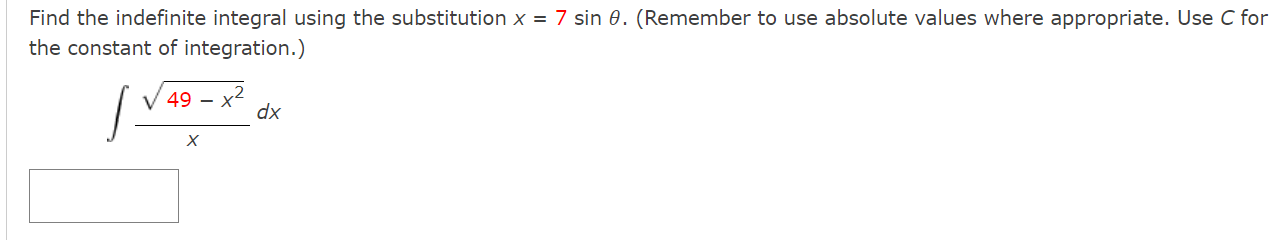









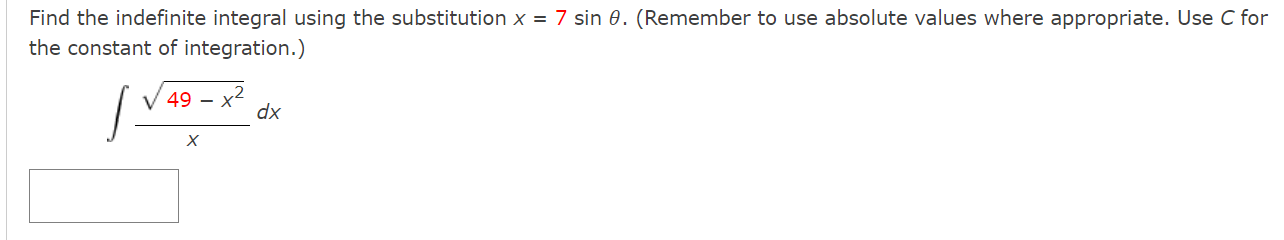







![25]. I Determine whether it diverges or converges. converges O diverges V](https://s3.amazonaws.com/si.experts.images/answers/2024/06/66657ffb566c6_93166657ffb45724.jpg)
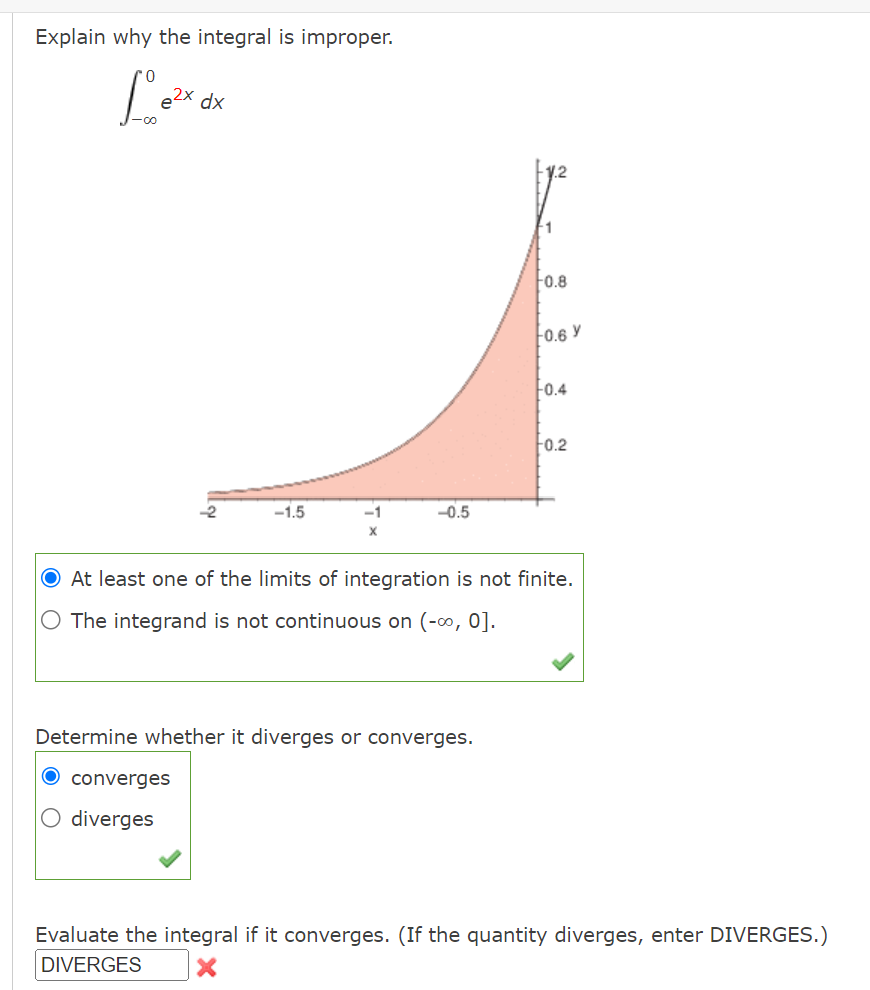

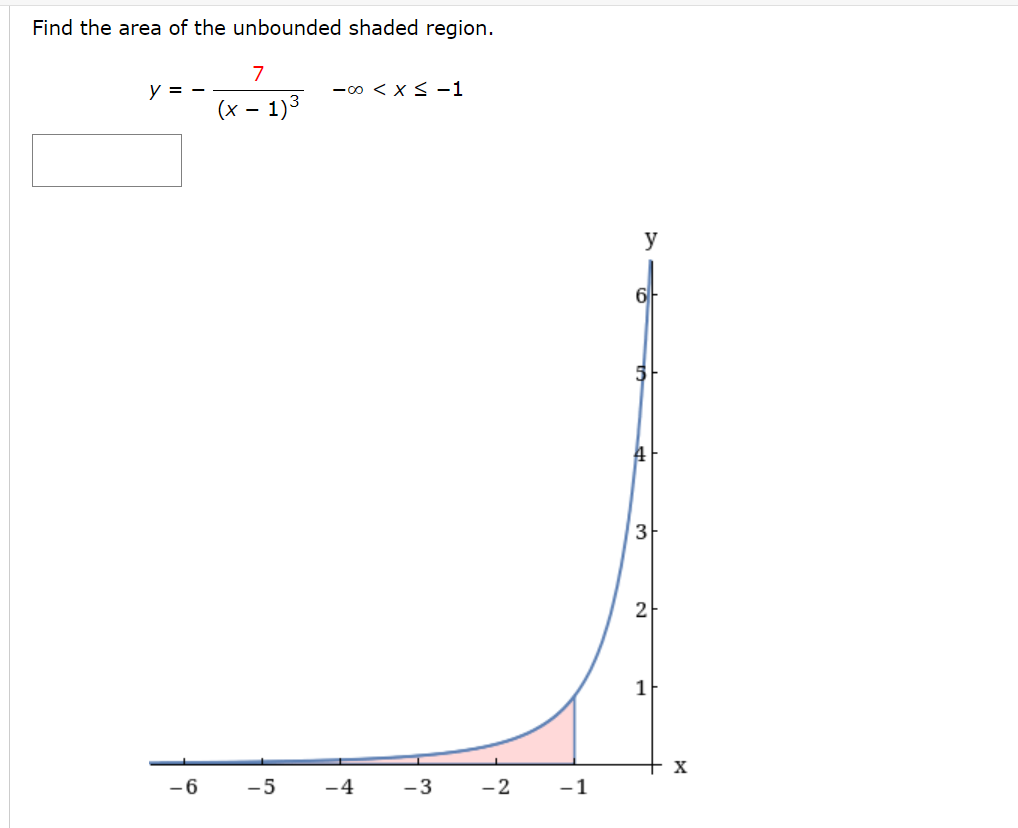
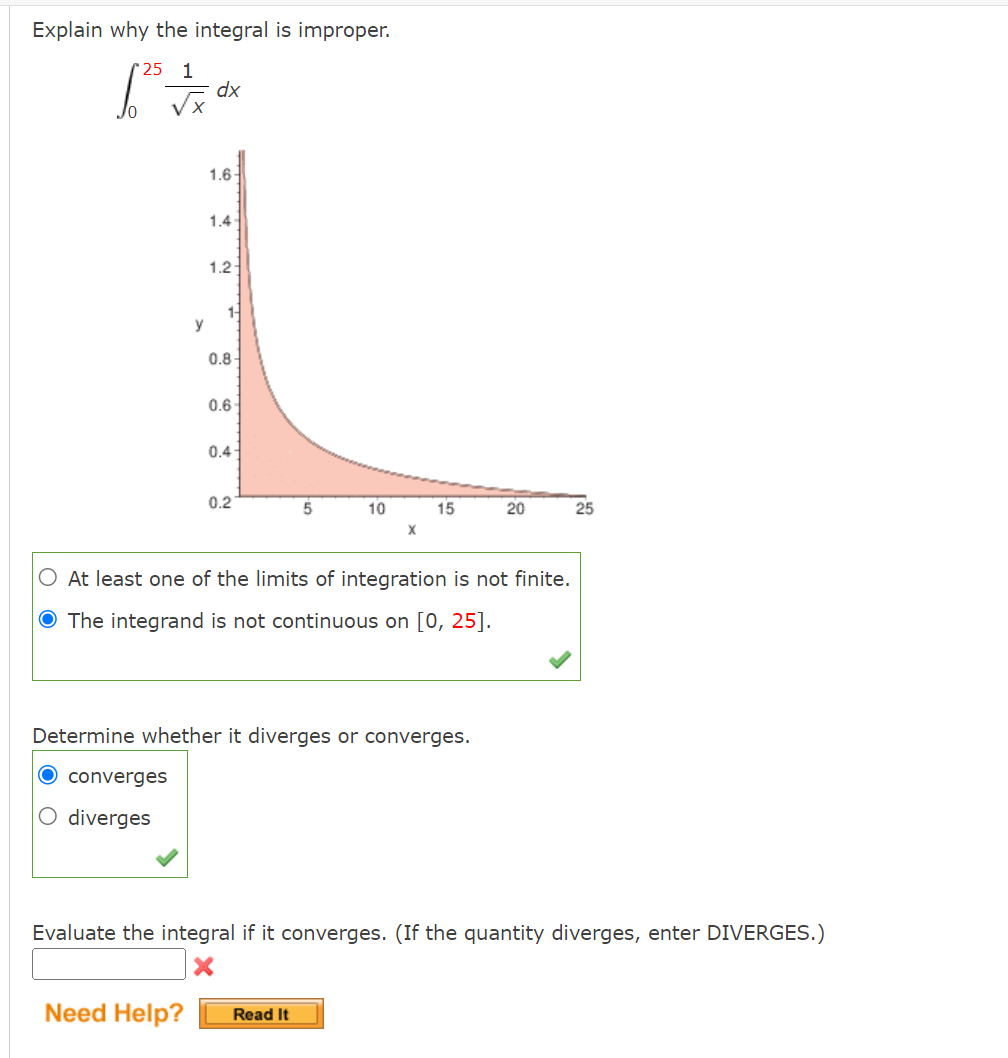
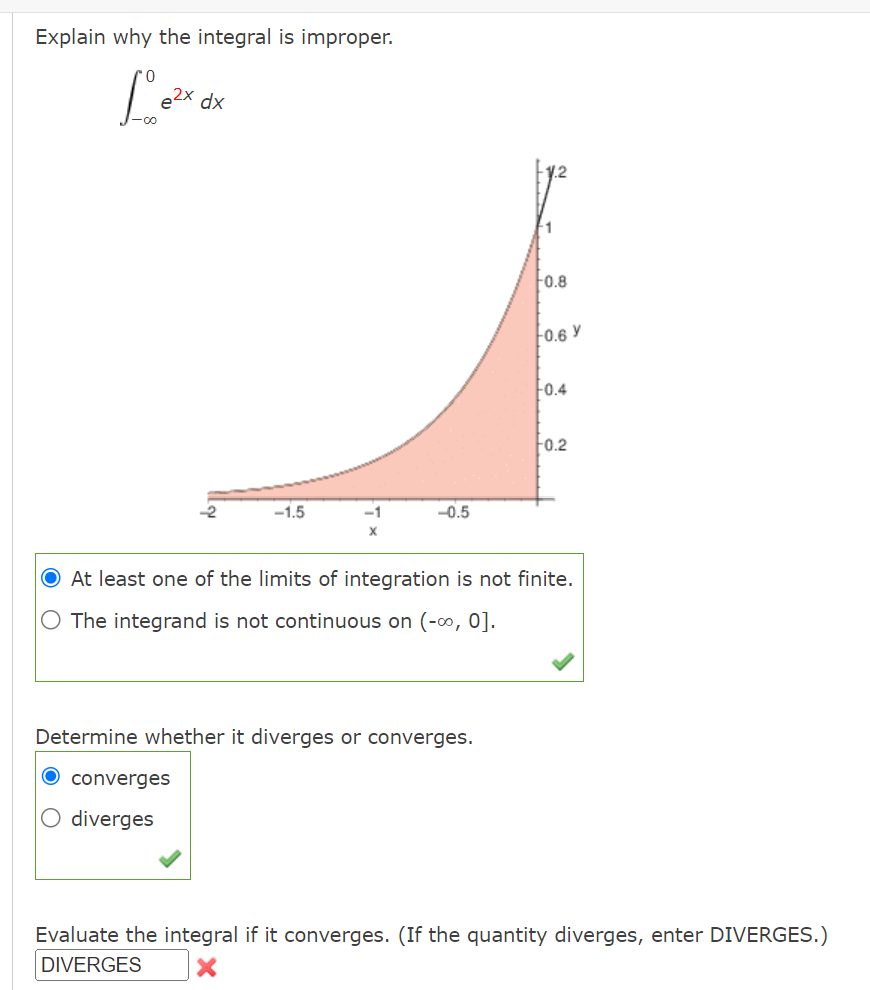
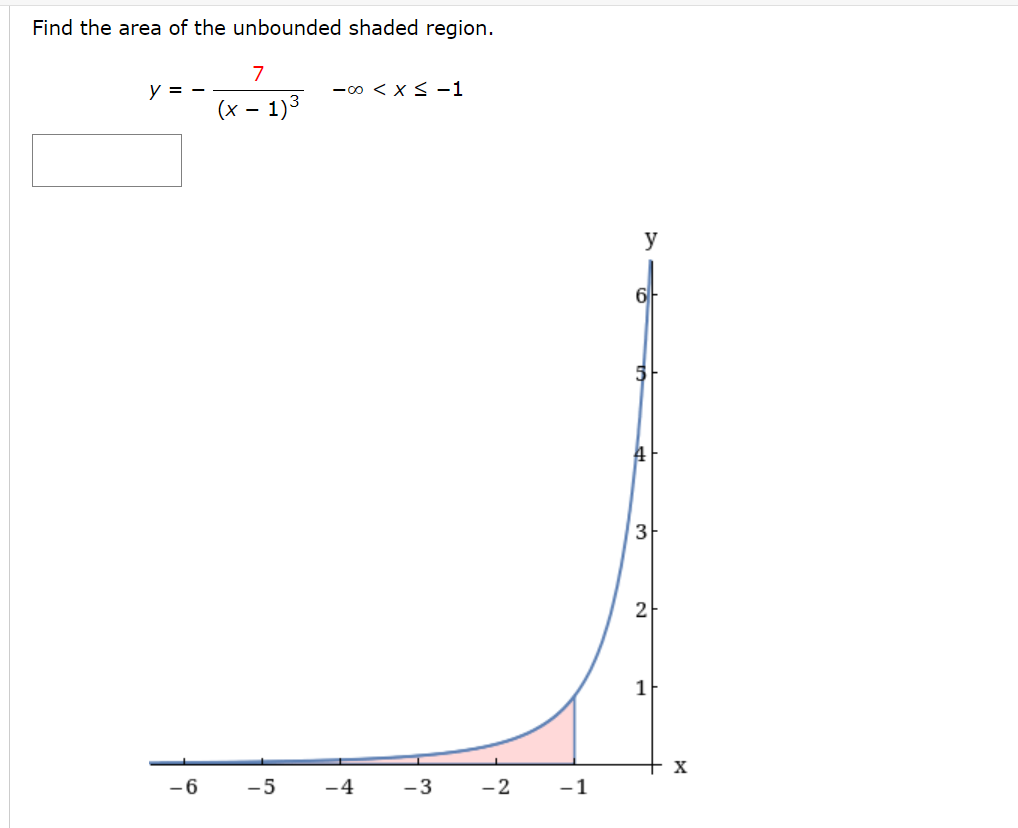
Complete the square and find the indefinite integral. (Use C for the constant of integration. ) x 2 dx 2x - x2Find the indefinite integral using the substitution x = 7 sin 0. (Remember to use absolute values where appropriate. Use C for the constant of integration.) 49 - X- dx XFind the indefinite integral by using the substitution x = 4 tan(9). (Use C for the constant of integration.) 2 [L dX (16 + x2)2 S Use the Special Integration Formulas (Theorem 8.2) to find the indefinite integral. (Remember to use absolute values where appropriate. Use C for the constant of integration.) 26x2 - 1 dx XUse partial fractions to evaluate the definite integral. Use a graphing utility to verify your result. Use a table of integrals to find the indefinite integral. (Use C for the constant of integration.) / 2 , dX .. 3x\" x4 1 Use a table of integrals to find the indefinite integral. (Use C for the constant of integration.) 19ex arccos( e 19x) dx XUse a table of integrals to find the indefinite integral. (Remember to use absolute values where appropriate. Use C for the constant of integration.) [X2 V" 3 + 4x2 dX Use a table of integrals to find the indefinite integral. (Use C for the constant of integration.) dx (4 - 2x) 3/2Explain why the integral is improper. 251 idx 0 \\/)_( 1.6 1.4 1.2 0.3 0.6 0.4 \"-2 5 1o 15 20 25 X 0 At least one of the limits of integration is not nite. The integrand is not continuous on [0, 25]. I Determine whether it diverges or converges. converges O diverges V Evaluate the integral if it converges. (If the quantity diverges, enter DIVERGES.) X Need Help? Explain why the integral is improper. 0 52X dx '00 / cm as Y n; 0.2 C} At least one of the limits of integration is not nite. O The integrand is not continuous on (-00, O]. a? Determine whether it diverges or converges. converges O diverges I Evaluate the integral if it converges. (II: the quantity diverges, enter DIVERGES.) DIVERGES x Determine whether the improper integral diverges or converges. 00 1 / 9dX 2 X\" converges O diverges V Evaluate the integral if it converges. (If the quantity diverges, enter DIVERGES.) X
Step by Step Solution
There are 3 Steps involved in it

Get step-by-step solutions from verified subject matter experts


