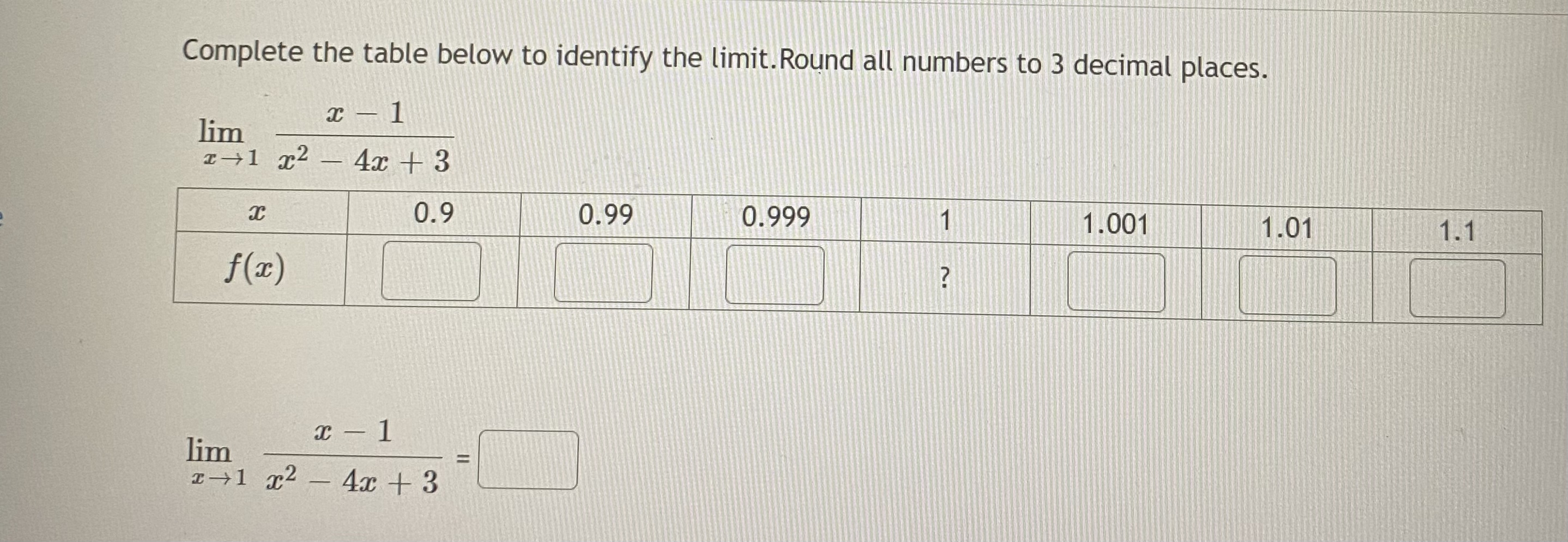
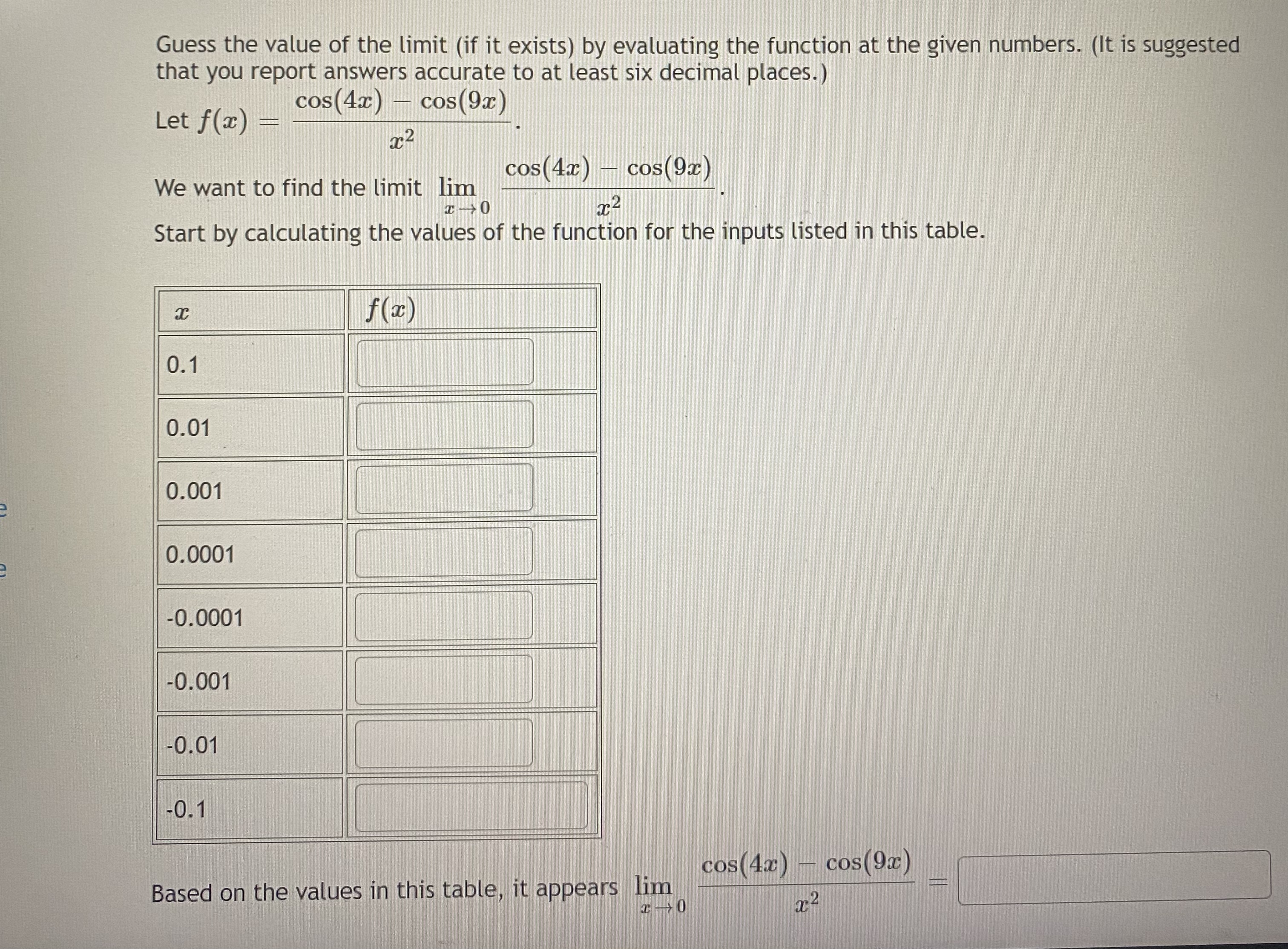
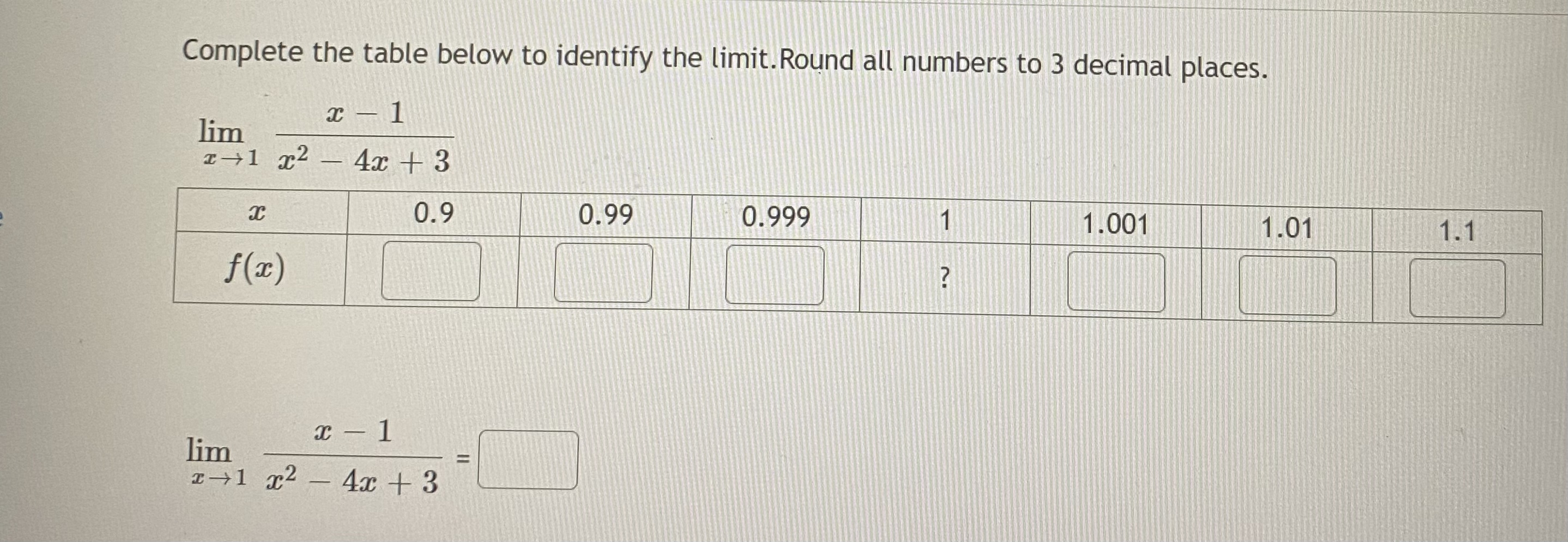
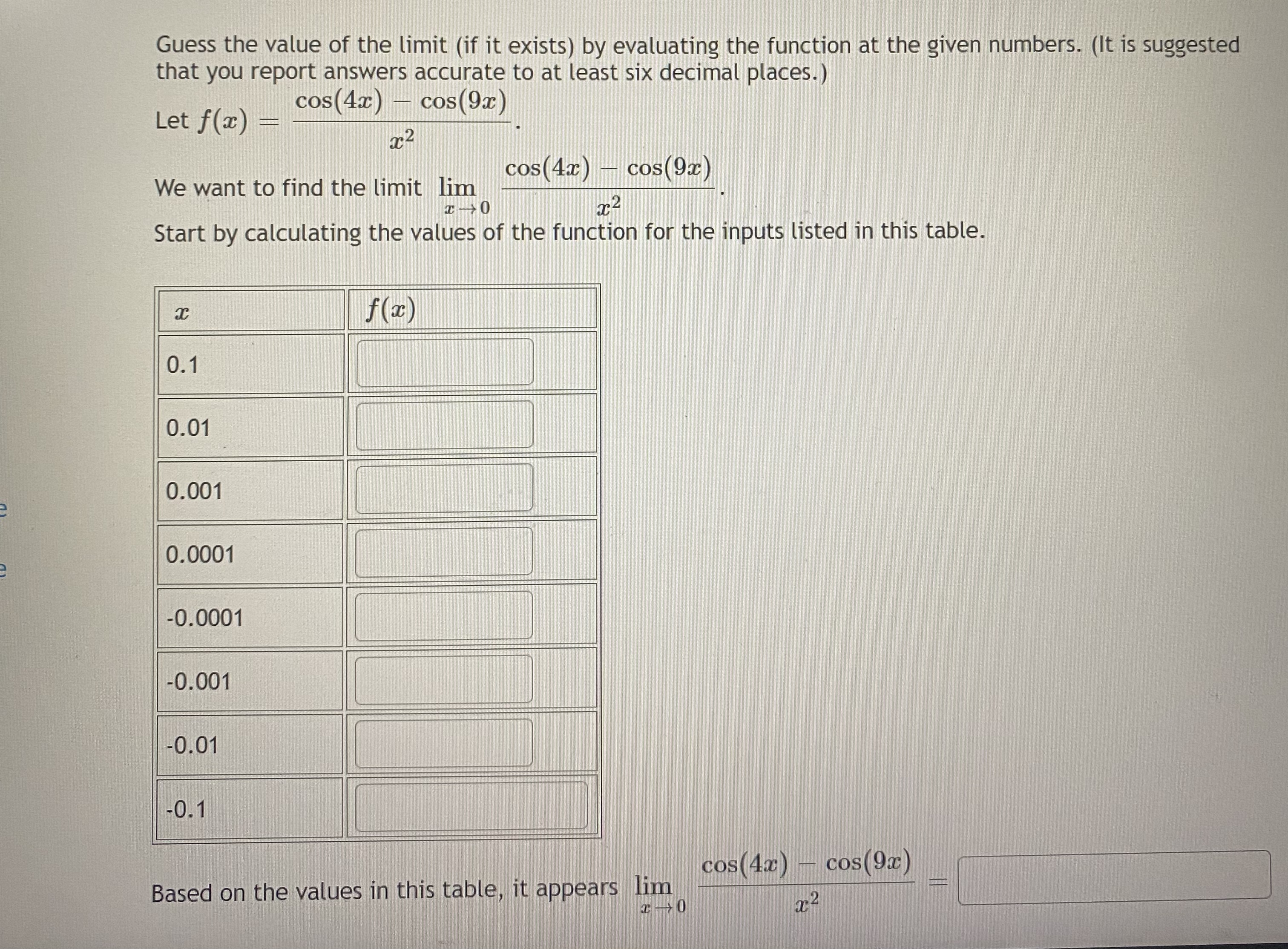
Complete the table below to identify the limit. Round all numbers to 3 decimal places. x - 1 lim 1-1 x2 - 4x + 3 0.9 0.99 0.999 1.001 1.01 1.1 f(x) x- 1 lim -+1 2 - 4x + 3ents Estimate the limit numerically or state that the limit does not exist: ous 97 - 1 lim ac Give your answer to at least three decimal placesGuess the value of the limit (if it exists) by evaluating the function at the given numbers. (It is suggested that you report answers accurate to at least six decimal places.) Let f (ac) cos (4x) - cos (9x) 5 2 We want to find the limit lim cos (4x) cos(9x) 2c2 Start by calculating the values of the function for the inputs listed in this table. f(z) 0.1 0.01 0.001 0.0001 -0.0001 -0.001 -0.01 -0.1 cos (4x) cos (9x) Based on the values in this table, it appears limConsider f(x) = x2 - 25 x - 5 ac f(x) f(z) 4.9 9.9 5.1 10.1 4.99 5.01 4.999 5.001 4.9999 5.0001 Looking at the values, we can estimate that lim f(a) = I- 5labus 9 Consider f (x) 3 f (x) 2.9 3.001 2.99 3.01 ols 2.999 3.1 kstore Looking at the values, we can estimate that lim f (x) = kstore ->3