Complete these simple exercises

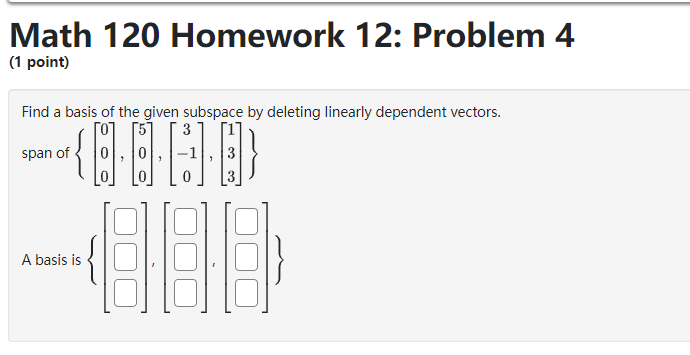
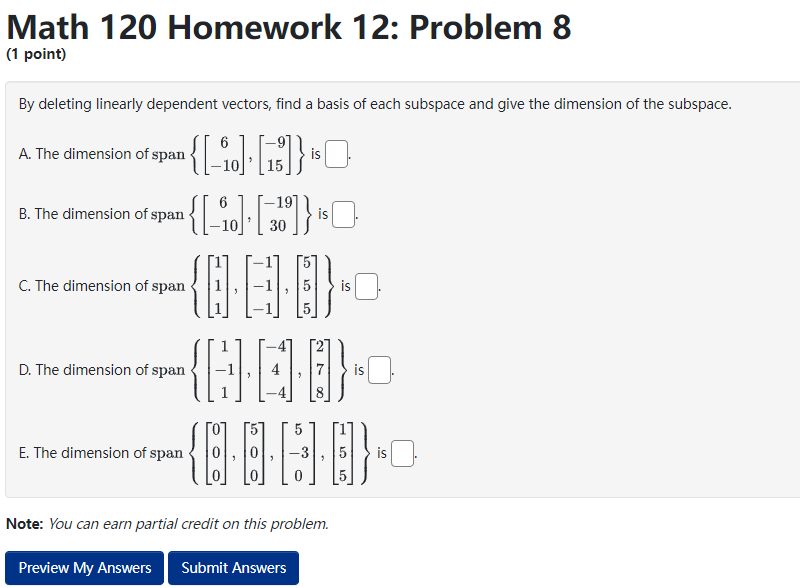
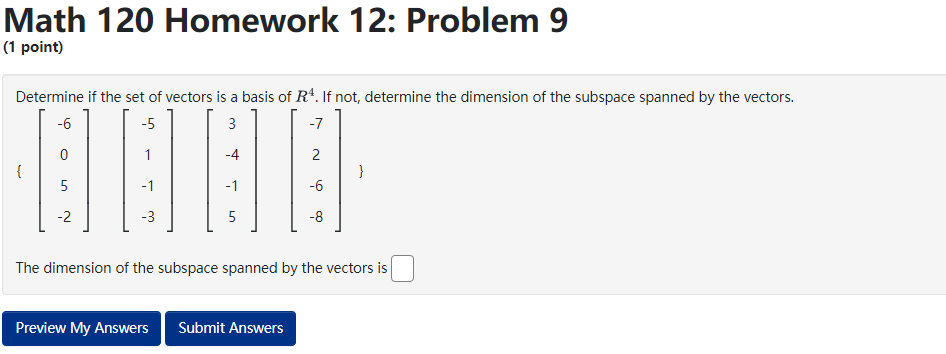
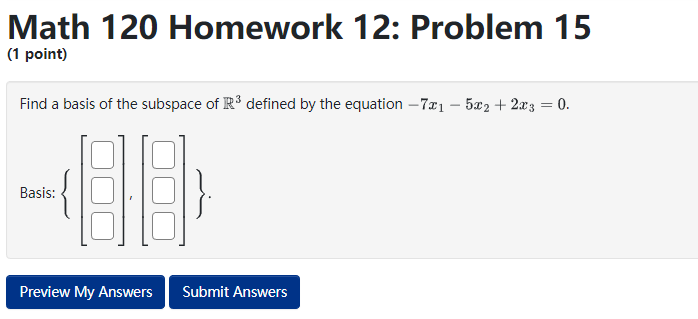
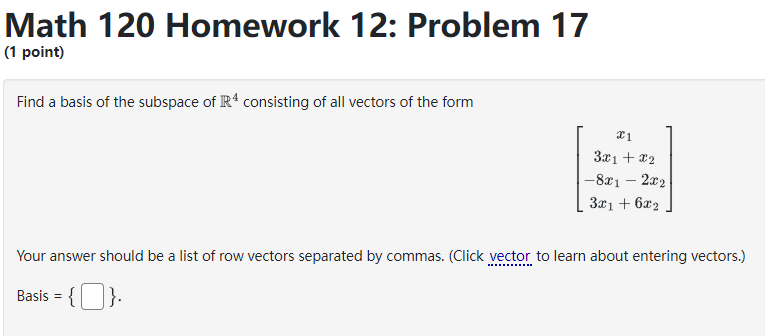
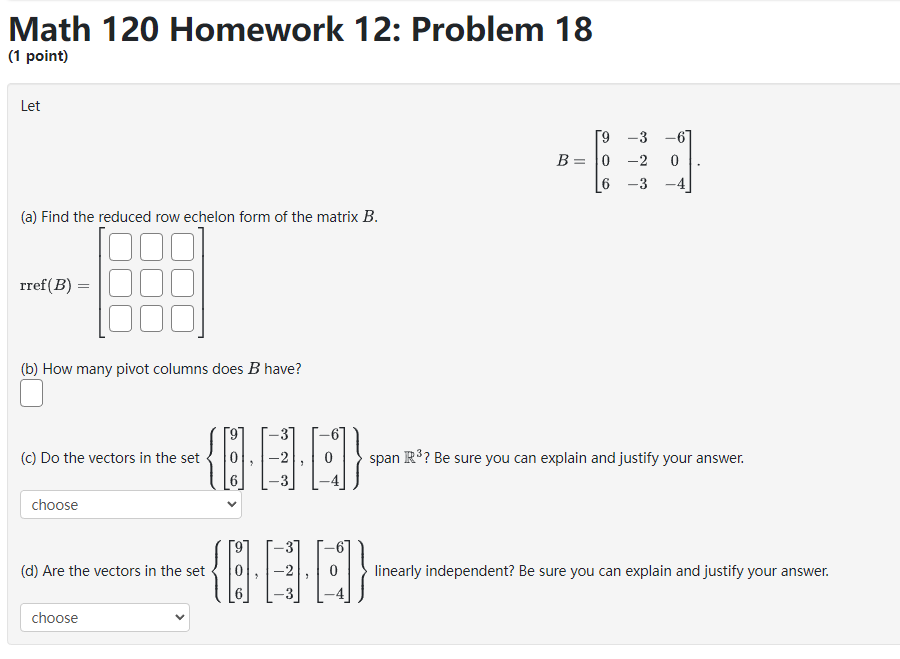
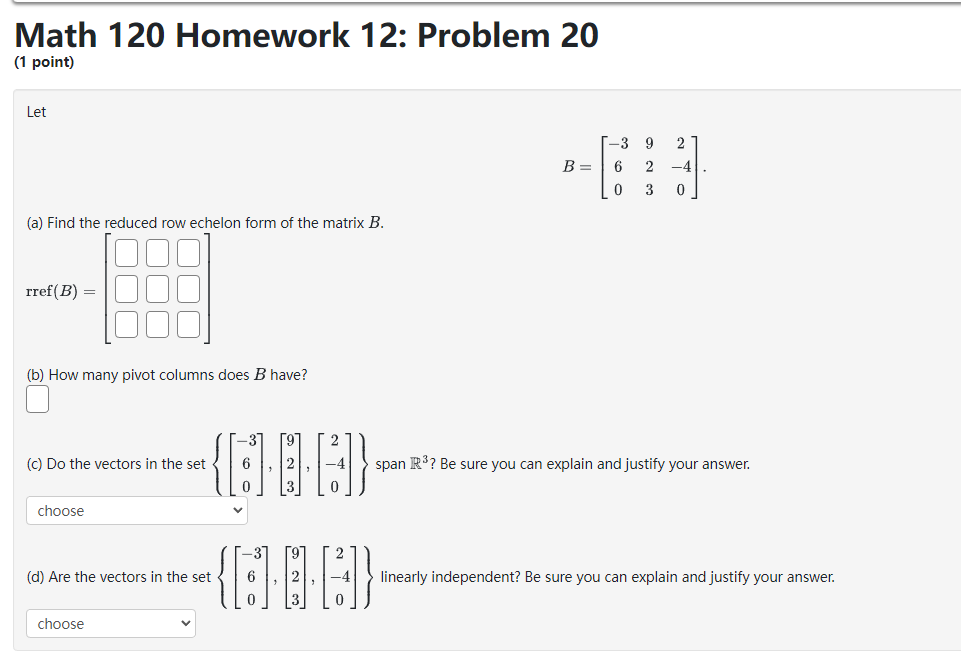
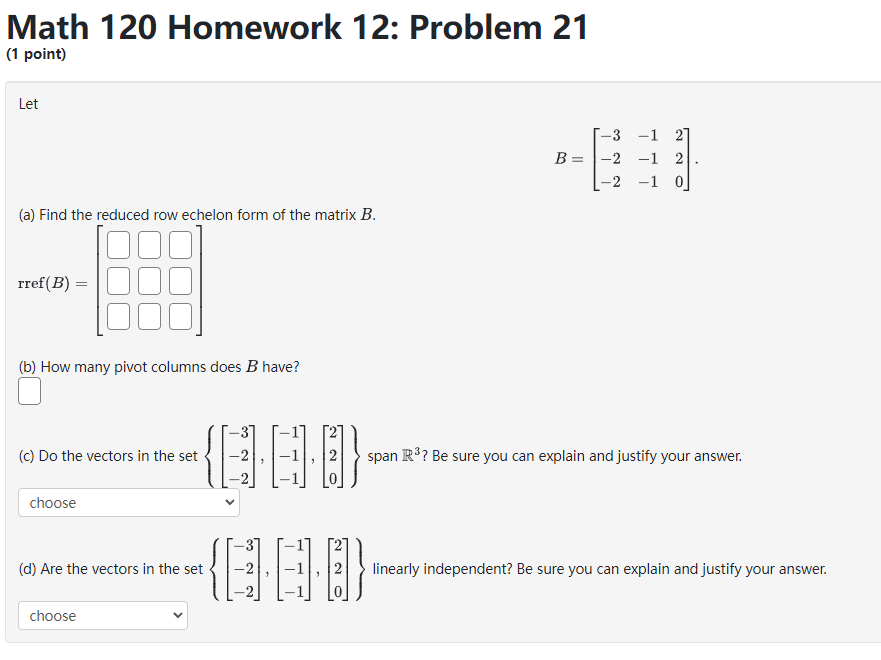
Math 120 Homework 12: Problem 3 (1 point) Suppose that S, and S, are subspaces of R', with dim(S1) = m, and dim($2) = my. If S, and S, have only 0 in common, then the maximum value of my + my is Preview My Answers Submit AnswersMath 120 Homework 12: Problem 4 (1 point) Find a basis of the given subspace by deleting linearly dependent vectors. Span of $ a. a. SAY A basis is BIBLEMath 120 Homework 12: Problem 7 (1 point} Determine if the set of 1r-rectors is a basis of E5. If not, determine the dimension of the subspace spanned by the vectors. 2 -2 4 -4 2 2 II} 2 2 4 { 2 2 4 4 -2 } 2 4 2 2 0 2 -2 4 4 2 The dimension of the subspace spanned by the vectors is || Math 120 Homework 12: Problem 8 (1 point) By deleting linearly dependent vectors, find a basis of each subspace and give the dimension of the subspace. A. The dimension of span to , } B. The dimension of span . . . [ ]}0 C. The dimension of span D. The dimension of span t. The dimension of span go , o . s .}- Note: You can earn partial credit on this problem. Preview My Answers Submit AnswersMath 120 Homework 12: Problem 9 (1 point) Determine if the set of vectors is a basis of R4. If not, determine the dimension of the subspace spanned by the vectors. 6 5 3 ? 0 \"i 4 2 { } 5 1 1 6 -2 -3 5 -8 The dimension of the subspace spanned by the vectors is ll Preview My Answers Math 120 Homework 12: Problem 15 (1 point) Find a basis of the subspace of R* defined by the equation -7c1 - 512 + 2x3 = 0. Basis: Preview My Answers Submit AnswersMath 120 Homework 12: Problem 16 (1 point} The vectors form a basis for R3 if and only if k % || Math 120 Homework 12: Problem 17 [1 point] Find a basis ofthe subspace of 1&4 consisting of all 1\"rectors of the form '31 3331 + $2 E:t.'1 21:2 3331 + 6.122 'i'our answer should be a list of rota.r vectors separated by commas. [Click _1_.{t_e_c_t_o_r_ to learn about entering 1sectors.) Basis = {|:| }. Math 120 Homework 12: Problem 18 (1 point) Let B = (a) Find the reduced row echelon form of the matrix B. 100 rref ( B) = (b) How many pivot columns does B have? (c) Do the vectors in the set { o . -2 . } span R*? Be sure you can explain and justify your answer. choose (d) Are the vectors in the set linearly independent? Be sure you can explain and justify your answer. chooseMath 120 Homework 12: Problem 19 (1 point) Let 25 -8 19 B = -4 13 5 -2 (a) Find the reduced row echelon form of the matrix B. 000 rref ( B) = (b) How many pivot columns does B have? -8 25 -8 19 (c) Do the vectors in the set -4 13 span R*? Be sure you can explain and justify your answer. 5 -2 choose (d) Are the vectors in the set " . # . [81] linearly independent? Be sure you can explain and justify your answer. choose Note: You can earn partial credit on this problem.Math 120 Homework 12: Problem 20 (1 point} Let 3 9 2 B: 6 2 4 , D 3 t] [a] Find the reduced rout.r echelon form ofthe matrix B. rref[3]= I II II I [b] How man},r pivot columns does 8 have? 3 9 2 [c] Do the vectors in the set { |: 6 :| , [2], [4] } span 2R3? Be sure you can explain andjustify your answer. choose v 3 9 {cl} Are the vectors in the set { |: 6 :| , [2], I] 3 choose v 2 [4] } linearly independent? Be sure you can explain and justify your answer. [I Math 120 Homework 12: Problem 21 (1 point) Let B = -2 -1 2 -2 -1 (a) Find the reduced row echelon form of the matrix B. 100 rref ( B) = (b) How many pivot columns does B have? (c) Do the vectors in the set choose (d) Are the vectors in the set linearly independent? Be sure you can explain and justify your answer. chooseMath 120 Homework 12: Problem 22 (1 point) Let 3 B = 1 -1 " do 7 4 1 (a) Find the reduced row echelon form of the matrix B. rref ( B) = 18888 (b) How many pivot columns does B have? (c) Do the vectors in the set span R ? Be sure you can explain and justify your answer. choose (d) Are the vectors in the set (1 4 . . linearly independent? Be sure you can explain and justify your answer. choose