Complex class(attached) enables operations on so called complex numbers. These are numbers of the form realPart + imaginaryPart * i, where i has the value of square root -1

The following are requirement for this assignment.

a). Modify the class to enable input and output of complex numbers through the overloaded >> and > operator provides the ability to change the private data members of the Complex class object.

b). Overload the multiplication operator to enable multiplication of two complex numbers as in algebra.

c). Overload the division operator to enable division of two complex numbers as in algebra. In here we need handle divide by zero situation.

d). Overload the == and != operators to allow comparisons of complex numbers.

e).Overload the = operator to allow assign a Complex object to the other Complex object.

f) Create CISP400V10A5.cpp to test all the functions designed in the assignment.

The following is an explanation on the complex number calculation.

Adding two complex numbers. The real parts are added together and the imaginary parts are added together. So, if we have (a + bi) + (c + di)), the result should be (a + c) + (b + d) i.

Subtracting two complex numbers. The real part of the right operand is subtracted from the real part of the left operand, and the imaginary part of the right operand is subtracted from the imaginary part of the left operand. So, if we have (a + bi) - (c + di)), the result should be (a - c) + (b - d) i.

Multiplying two complex numbers. The real part of the result is the real part of the right operand multiplies the real part of the left operand minus the imaginary part of the right operand multiply the imaginary part of the left operand. The imaginary part of the result is the real part of the left operand multiply the imaginary part of the left operand plus the imaginary part of the left operand multiply the real part of the right operand. So, if we have (a + bi) * (c + di)), the result should be (ac - bd) + (ad + bc) i.

Dividing two complex numbers. We set the value of square real part of the denominator plus square imaginary part of the denominator is A. The real part of the result is the real part of the numerator multiplies the real part of the denominator plus the imaginary part of the numerator multiply the imaginary part of the denominator and divided by A. The imaginary part of the result is the real part of the left operand multiply the imaginary part of the left operand plus the imaginary part of the left operand multiply the real part of the right operand. So, if we have (a + bi) / (c + di)), the result should be (ac+bd)+i(bc-ad))/(c²+d²).

If you have question regarding the calculation of complex numbers you can refer to Complex numbers.doc file which is attached with this assignment. Or you can search the internet for information.

CISP400V10A5.cpp

In CISP400V10A5.cpp we need to do the following

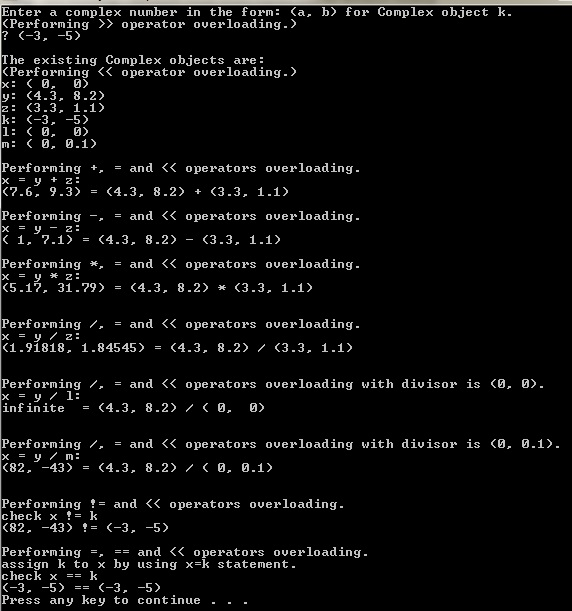
Instantiate 6 Complex objects ( x, y( 4.3, 8.2 ), z( 3.3, 1.1 ), k, l, and m(0, 0.1)).

Use cin >> k: statement to provide k object data.

Display all the object data by using cout

Use x = y + z; statement to demonstrate overloading + and = operators. And use cout

Use x = y - z; statement to demonstrate overloading - and = operators. And use cout

Use x = y * z; statement to demonstrate overloading * and = operators. And use cout

Use x = y / z; statement to demonstrate overloading / and = operators. And use cout

Use x = y / l; statement to demonstrate overloading / and = operators. And use cout

Use x = y / m; statement to demonstrate overloading / and = operators. And use cout

Use if ( x != k ) cout

Use x = k; statement to demonstrate overloading = operator.

Use if (x == k ) cout

The assignment comes with a CISP400V10A5.zip file. It includes four files (CISP400V10A5.exe, Complex.h, Complex.cpp, and fig10_16.cpp). The CISP400V10A5.exe file is an executable file. You can double click the file to get to the expecting result (see the picture below) of this assignment. The Complex.h, Complex.cpp, and fig10_16.cpp are files coming from the textbook examples which you can use so you dont need to start from scratch. You also need to follow the specification for the CISP400V10A5.cpp to do the driver to test the Complex class. After you finish your implementation for the Complex class and CISP400V10A5.cpp, you can put the CISP400V10A5.cpp, Complex.h and Complex.cpp in a project and then you can run to the same result as the CISP400V10A5.exe.

-------------------------------------------------------------------------------------

// Complex.cpp // Complex class member-function definitions. #include #include "Complex.h" // Complex class definition using namespace std;

// Constructor Complex::Complex( double realPart, double imaginaryPart ) : real( realPart ), imaginary( imaginaryPart ) { // empty body } // end Complex constructor

// addition operator Complex Complex::operator+( const Complex &operand2 ) const { return Complex( real + operand2.real, imaginary + operand2.imaginary ); } // end function operator+

// subtraction operator Complex Complex::operator-( const Complex &operand2 ) const { return Complex( real - operand2.real, imaginary - operand2.imaginary ); } // end function operator-

// display a Complex object in the form: (a, b) void Complex::print() const { cout

-------------------------------------------------------------------------

// Complex.h // Complex class definition. #ifndef COMPLEX_H #define COMPLEX_H

class Complex { public: explicit Complex( double = 0.0, double = 0.0 ); // constructor Complex operator+( const Complex & ) const; // addition Complex operator-( const Complex & ) const; // subtraction void print() const; // output private: double real; // real part double imaginary; // imaginary part }; // end class Complex

#endif

---------------------------------------------------------------------------

// V10A5.cpp // Complex class test program. #include #include "Complex.h" using namespace std;

int main() { Complex x; Complex y( 4.3, 8.2 ); Complex z( 3.3, 1.1 );

cout

x = y + z; cout

x = y - z; cout

Enter a complex number in the form (a b> for Complex object k XPerforming operator overloading. X-3 The existing Complex objects are: (Performing operator overloading. y: (4.3 8.2 z (3.3 1.1 (-3 0-1 Performing an operators overloading. 2 (7.6 9.3 (4.3 8.2 (3.3 1.1 Performing and KK operators overloading X 1 7.1 (4.3 8-2 (3.3 1.1 Performing and KK operators overloading (5.17 31.79) 4.3. 8.2 K3.3. 1.1 2 Performing and operators overloading. K4.3. 8.2> (1.91818 1.84545 Performing an KK operators overloading with divisor is (0, a infinite Performing and operators overloading with divisor is (0, 0.1 (82 43 K4.3, 8.2 K 0, 0.1 Performing k" and operators overloading. check x (82 43) (-3 Performing and operators overloading. assign k to x by using x-k statement check x X-3 (-3 Press any key to continue