Complexity questions!!!

As an upgrade to your program, more complex calculations can be processed and the outputs of

calculations can be sent directly to a financial analysis program to aid in generating automated financial reports. There are concerns by your superiors about outputs of calculations being lost in transit from

your calculator program to the financial analysis program which could lead to errors in the

automatically-generated financial report. Explain to your superiors how the operating system will

ensure there is no loss in transmitted information from the calculator program to the financial analysis

program

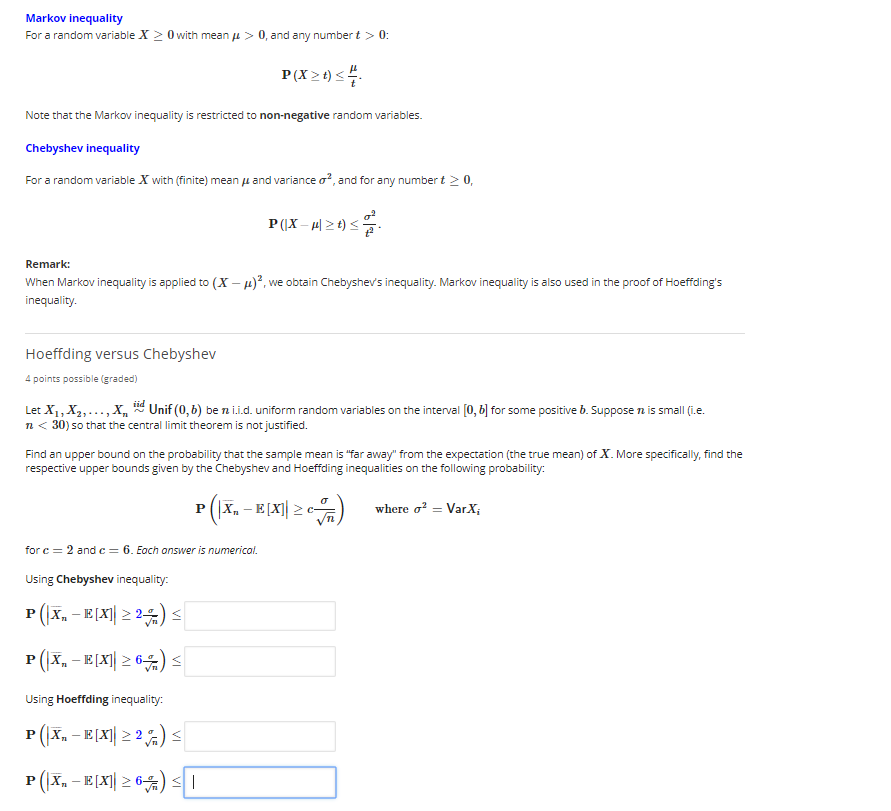
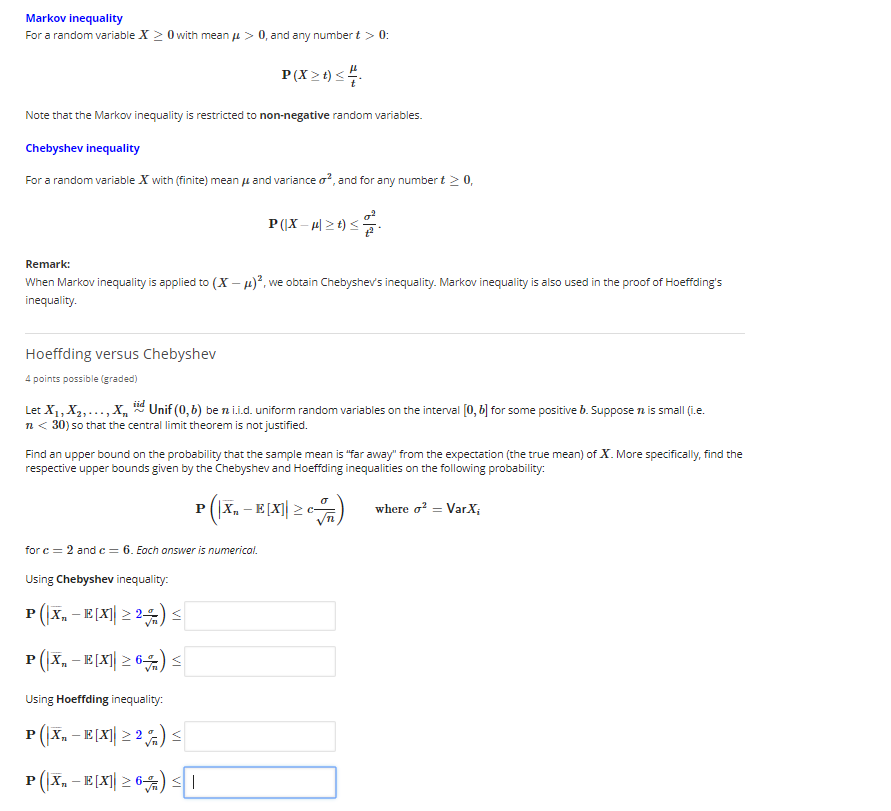
Figure 1.2 4.0 Grades in Economics (G.P.A) 4.0 Grades in English (G.P.A) The PPC in Figure 1.2 indicates a student who: a. is equally proficient in Economics and English. O b. is more proficient at Economics than English O c. prefers Economics over English. d. is more proficient at English than Economics. e. prefers English over Economics.Markov inequality For a random variable X 2 0 with mean / > 0, and any numbert > 0: P (X > D). Note that the Markov inequality is restricted to non-negative random variables. Chebyshev inequality For a random variable X with (finite) mean / and variance of, and for any number t 2 0, P(X -/| 20) . Remark: When Markov inequality is applied to (X - ()", we obtain Chebyshev's inequality. Markov inequality is also used in the proof of Hoeffding's inequality. Hoeffding versus Chebyshev 4 points possible (graded) Let X1, X2, ..., X'n " Unif (0, b) be ni.i.d. uniform random variables on the interval [0, b] for some positive b. Suppose n is small (i.e. 7