Composing linear pieces- computer science / neural networks / linear algebra

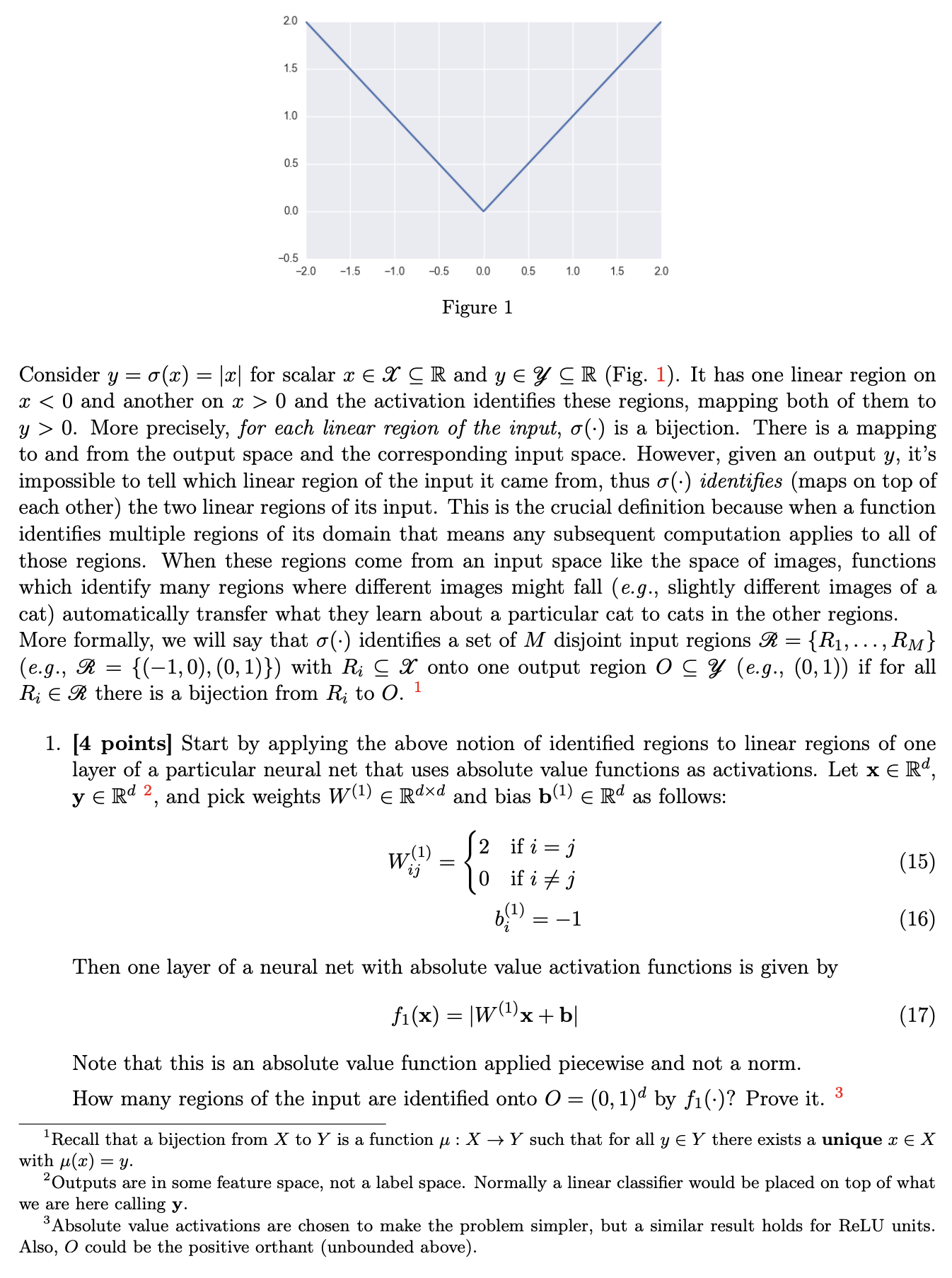
2.0 1.5 1.0 0,5 0.0 2.0 -1.5 -1.0 -0.5 0.0 0.5 1.0 1.5 2.0 Figure 1 Consider y = 0(3) = |x| for scalar m E .9.\" Q R and y E a g R (Fig. 1). It has one linear region on x O and the activation identies these regions, mapping both of them to y > 0. More precisely, for each linear region of the input, cr(-) is a bijection. There is a mapping to and from the output space and the corresponding input space. However, given an output 3;, it's impossible to tell which linear region of the input it came from, thus a(-) identies (maps on top of each other) the two linear regions of its input. This is the crucial denition because when a function identies multiple regions of its domain that means any subsequent computation applies to all of those regions. When these regions come from an input space like the space of images, functions which identify many regions where different images might fall (e.g., slightly different images of a cat) automatically transfer what they learn about a particular cat to cats in the other regions. More formally, we will say that 0(-) identies a set of M disjoint input regions .% = {R1, . . . ,RM} (e.g., 935 = {(1,0),(0,1)}) with R,- g 2' onto one output region 0 Q a (3.9., (0,1)) if for all R,- E 933 there is a bijection from R,- to O. 1 1. [4 points] Start by applying the above notion of identied regions to linear regions of one layer of a particular neural net that uses absolute value functions as activations. Let x 6 Rd, y 6 Rd 2, and pick weights W0) 6 Rd\" and bias ha) 6 Rd as follows: W(i)= 2 ifizj. (15) 3 0 if t 75 3 b?) = 1 (16) Then one layer of a neural net with absolute value activation functions is given by f1(x) = |W(1)x+ b| (17) Note that this is an absolute value function applied piecewise and not a norm. How many regions of the input are identied onto 0 = (0, 1)d by f1(-)? Prove it. 3 1Recall that a bijection from X to Y is a function ,u z X ) Y such that for all y E Y there exists a unique 9: E X with \"(1') = y. 2Outputs are in some feature space, not a label space. Normally a linear classier would be placed on top of what we are here calling y. 3Absolute value activations are chosen to make the problem simpler, but a similar result holds for ReLU units. Also, 0 could be the positive orthant (unbounded above)