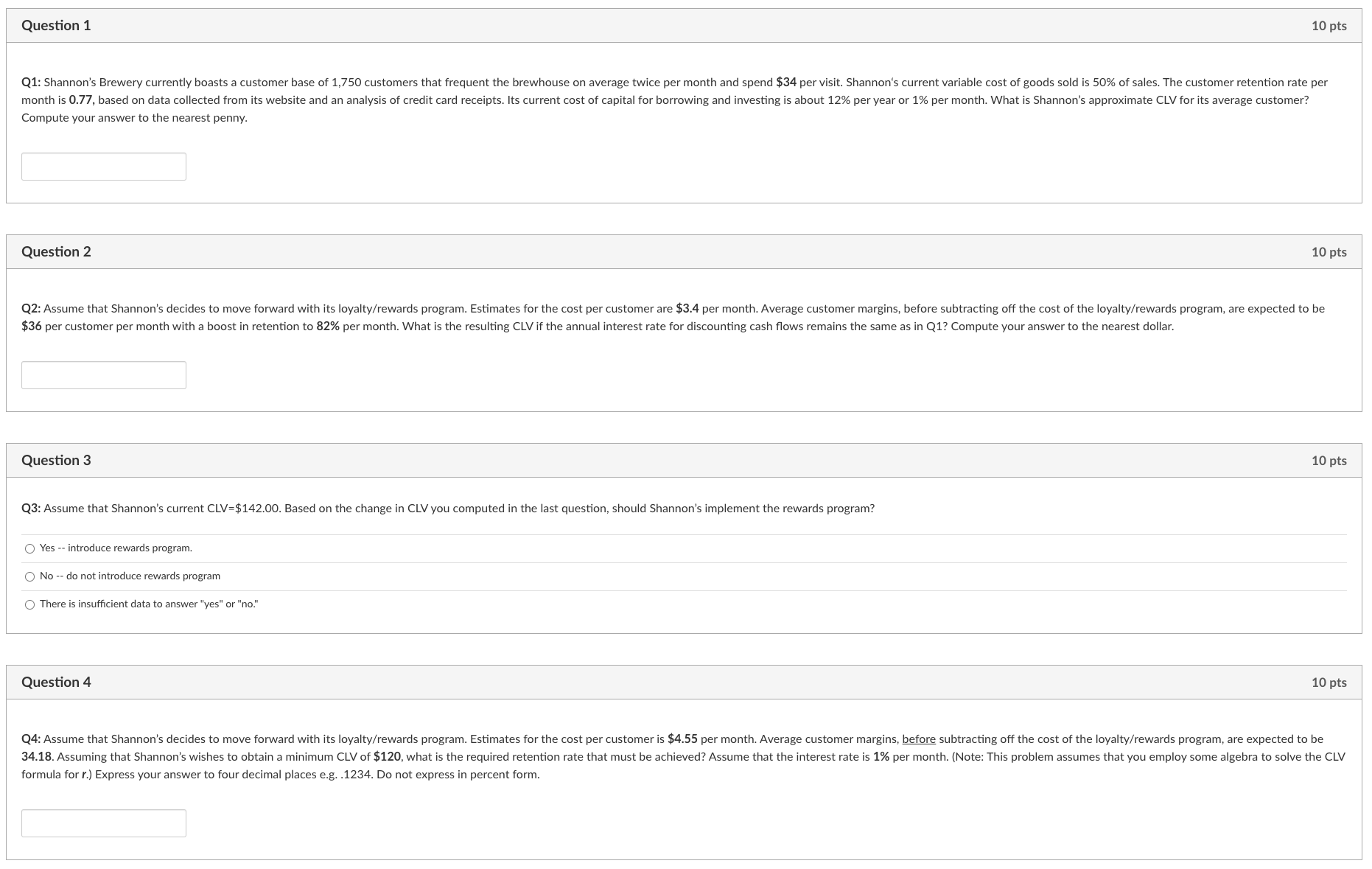
computation. These three input variables should make sense: the customer and the variable costs needed to retain that customer. - The retention rate (r) is the probability that a given customer will be retained for the period analyzed. - The interest rate used for discounting future cash flows from the customer to their present values. The formula capturing the relationships between these variables is: (1) CLV=$M[1+ir1] CLV = Customer Lifetime Value $M= Customer cash margin per period r= Customer retention rate per period i= Discount rate per period. 1% per month. Should the increased investment in the loyalty program be made? The CLV for the current loyalty program is: (2) CLV=$M[1+ir1]=$36[1+.01.751]=$138.46 The CLV anticipate based on the revised loyalty program is: (3) CLV=$M[1+ir1]=($37.50$3.50)[1+.01.81]=$161.90 of $160. The resulting algebraic equation is: (4) r=1+iCLV$M (5) r=1+.01$138.46$34=.7644 or 76.44% Compute your answer to the nearest penny. Question 2 10 pts Question 3 10pts Q3: Assume that Shannon's current CLV=$142.00. Based on the change in CLV you computed in the last question, should Shannon's implement the rewards program? Yes -- introduce rewards program. No -- do not introduce rewards program There is insufficient data to answer "yes" or "no." Question 4 10 pts formula for r.) Express your answer to four decimal places e.g. .1234. Do not express in percent form. .01 per month): (6) CLV=$M[1+ir1]=($50.00)[1+.01.751]=$192.31 (7) CLV=$M[1+ir1]=($47.50)[1+.01.81]=$226.19 question is how much must $M increase to achieve the same projected CLV of $226.19 if the retention rate remains r=.75 ? Solving equation (1) for $M yields: (8) $M=CLV(1+ir)=226.19(1+.01.75)=$58.81 the proposed rewards program's ability to increase sales and/or retention rates. margins on CLV can be estimated with a simple modification to Equation (1) which adds the growth rate to the retention rate in the denominator of the equation: (9) CLV=$M[1+irg1] For example, in Equation (7) if we assume the rewards program will have the further benefit of increasing customer margins by 1% per month ( g=.01 ), the net effect on CLV is: (10) CLV=$M[1+irg1]=($47.50)[1+.01.8.011]=$237.50 Clearly, a constant growth rate in average customer margins, even as small as 1% per period, can have a significant effect on CLV. It's Your Turn. Show Us What You Have Learned. and web promotions on its own website and Facebook page will be extensively employed to create buzz and disseminate promotion information. computation. These three input variables should make sense: the customer and the variable costs needed to retain that customer. - The retention rate (r) is the probability that a given customer will be retained for the period analyzed. - The interest rate used for discounting future cash flows from the customer to their present values. The formula capturing the relationships between these variables is: (1) CLV=$M[1+ir1] CLV = Customer Lifetime Value $M= Customer cash margin per period r= Customer retention rate per period i= Discount rate per period. 1% per month. Should the increased investment in the loyalty program be made? The CLV for the current loyalty program is: (2) CLV=$M[1+ir1]=$36[1+.01.751]=$138.46 The CLV anticipate based on the revised loyalty program is: (3) CLV=$M[1+ir1]=($37.50$3.50)[1+.01.81]=$161.90 of $160. The resulting algebraic equation is: (4) r=1+iCLV$M (5) r=1+.01$138.46$34=.7644 or 76.44% Compute your answer to the nearest penny. Question 2 10 pts Question 3 10pts Q3: Assume that Shannon's current CLV=$142.00. Based on the change in CLV you computed in the last question, should Shannon's implement the rewards program? Yes -- introduce rewards program. No -- do not introduce rewards program There is insufficient data to answer "yes" or "no." Question 4 10 pts formula for r.) Express your answer to four decimal places e.g. .1234. Do not express in percent form. .01 per month): (6) CLV=$M[1+ir1]=($50.00)[1+.01.751]=$192.31 (7) CLV=$M[1+ir1]=($47.50)[1+.01.81]=$226.19 question is how much must $M increase to achieve the same projected CLV of $226.19 if the retention rate remains r=.75 ? Solving equation (1) for $M yields: (8) $M=CLV(1+ir)=226.19(1+.01.75)=$58.81 the proposed rewards program's ability to increase sales and/or retention rates. margins on CLV can be estimated with a simple modification to Equation (1) which adds the growth rate to the retention rate in the denominator of the equation: (9) CLV=$M[1+irg1] For example, in Equation (7) if we assume the rewards program will have the further benefit of increasing customer margins by 1% per month ( g=.01 ), the net effect on CLV is: (10) CLV=$M[1+irg1]=($47.50)[1+.01.8.011]=$237.50 Clearly, a constant growth rate in average customer margins, even as small as 1% per period, can have a significant effect on CLV. It's Your Turn. Show Us What You Have Learned. and web promotions on its own website and Facebook page will be extensively employed to create buzz and disseminate promotion information