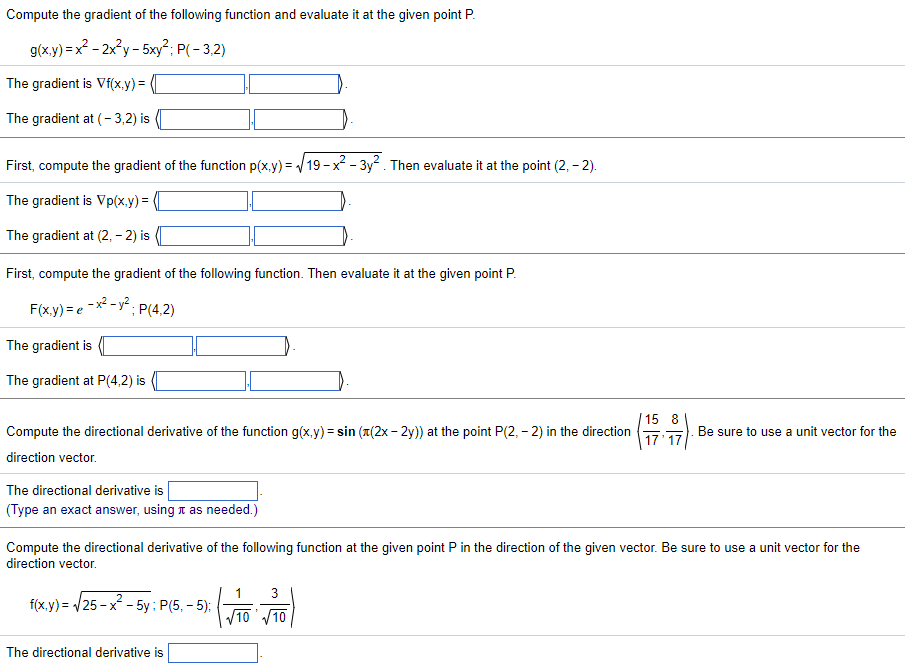
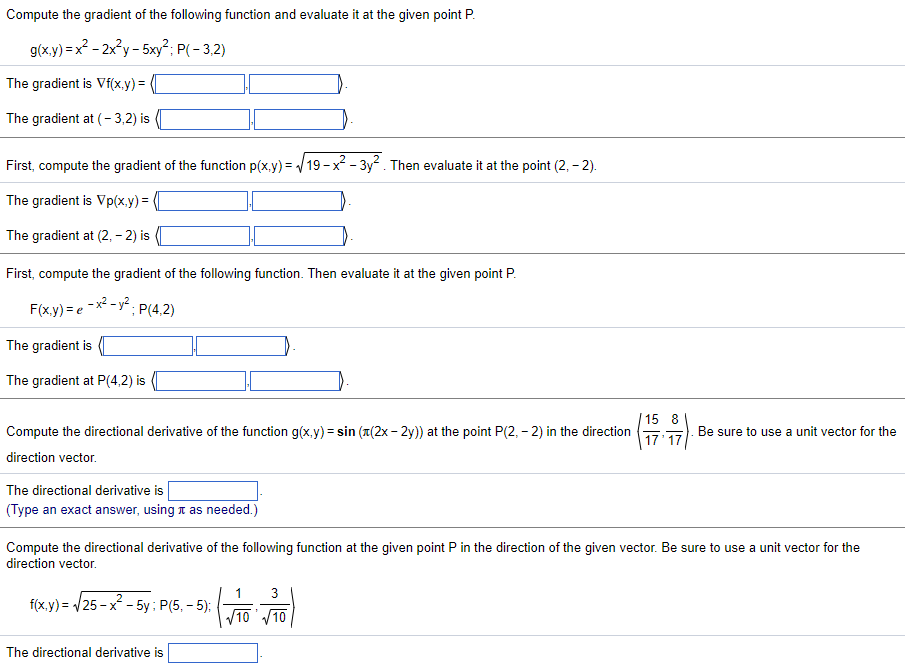
Compute the gradient of the following function and evaluate it at the given point P. g(x,y) =x - 2x y - 5xy2; P( - 3,2) The gradient is Vi(x.y) = ( The gradient at ( - 3,2) is (] First, compute the gradient of the function p(x.y) = :19 - x- - 3y . Then evaluate it at the point (2, - 2). The gradient is Vp(x,y) = ( The gradient at (2, - 2) is ( First, compute the gradient of the following function. Then evaluate it at the given point P. F(x,y ) = e - x2 - yz; P(4,2) The gradient is The gradient at P(4,2) is (] Compute the directional derivative of the function g(x,y) = sin (x(2x - 2y)) at the point P(2, - 2) in the direction 15 8 77 17) Be sure to use a unit vector for the direction vector. The directional derivative is (Type an exact answer, using it as needed.) Compute the directional derivative of the following function at the given point P in the direction of the given vector. Be sure to use a unit vector for the direction vector. f(x,y) = 25 -x- - 5y; P(5, - 5); 1 3 10 ' 10 The directional derivative is