computer science

Dev C$++$

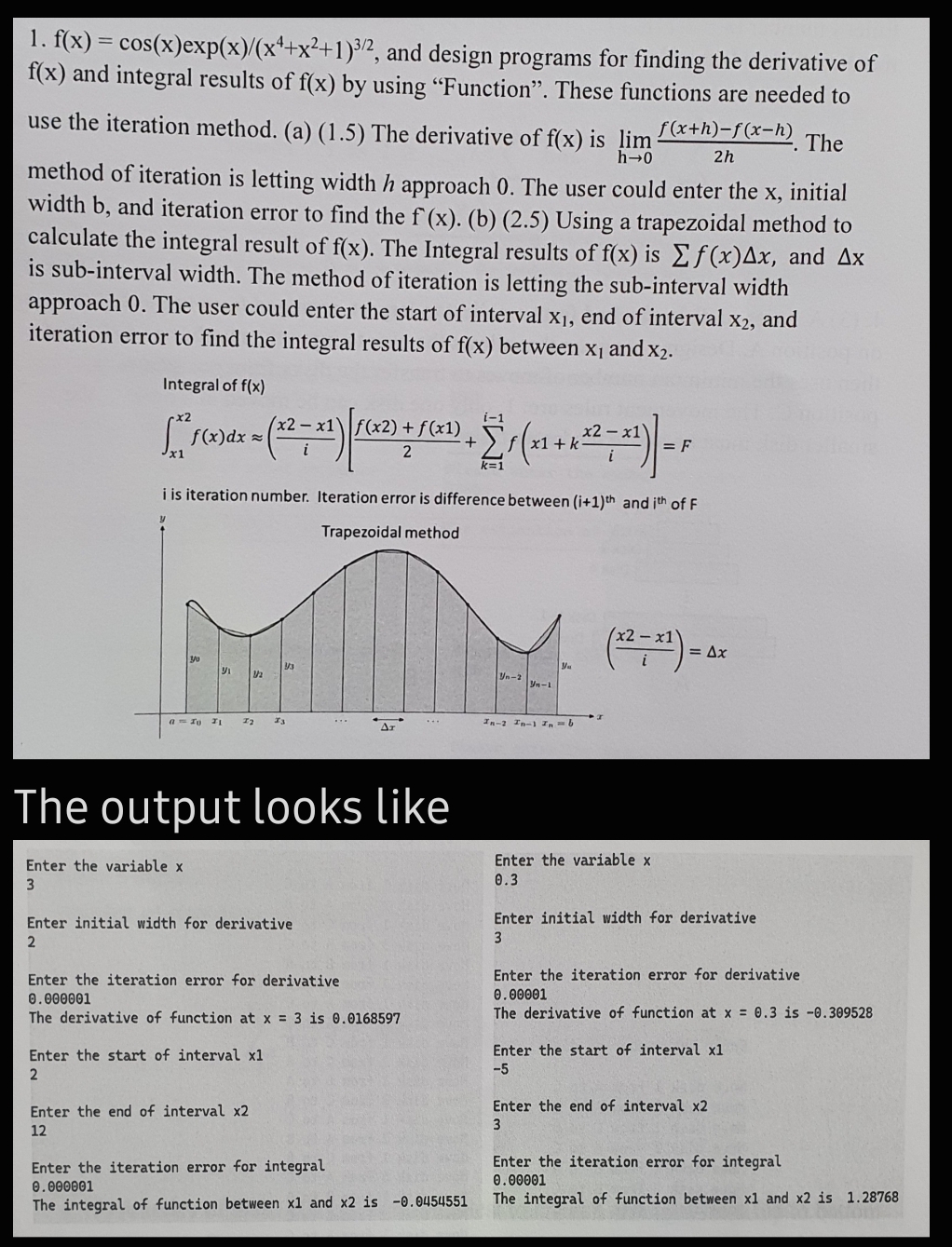
$f(x)=cos(x)exp\frac{x}{(x^4+x^2+1{)}^{\frac{3}{2}}},$ and design programs for finding the derivative of $f(x)$ and integral results of $f(x)$ by using "Function". These functions are needed to use the iteration method. $($a$)(1\mathrm{.}5)$ The derivative of $f(x)$ is $\underset{h0}{lim}\frac{f(x+h)-f(x-h)}{2h}.$ The method of iteration is letting width $h$ approach $0.$ The user could enter the $x,$ initial width $b,$ and iteration error to find the $f(x).($b$)(2\mathrm{.}5)$ Using a trapezoidal method to calculate the integral result of $f(x).$ The Integral results of $f(x)$ is ${\displaystyle \underset{?}{\overset{?}{}}}f(x)x,$ and $x$ is sub$-$interval width. The method of iteration is letting the sub$-$interval width approach $0.$ The user could enter the start of interval $x_1,$ end of interval $x_2,$ and iteration error to find the integral results of $f(x)$ between $x_1$ and $x_2.$

Integral of $f(x)$

${\displaystyle \underset{x1}{\overset{x2}{}}}f(x)dx$~~$(\frac{x2-x1}{i})[\frac{f(x2)+f(x1)}{2}+{\displaystyle \underset{k=1}{\overset{i-1}{}}}f(x1+k\frac{x2-x1}{i})]=F$

$i$ is iteration number. Iteration error is difference between $(i+1{)}^{th}$ and $i^{th}$ of $F$

The output looks like

Enter the variable $x$

$3$

Enter initial width for derivative

$2$

Enter the iteration error for derivative

$0\mathrm{.}000001$

The derivative of function at $x=3$ is $0\mathrm{.}0168597$

Enter the start of interval $x1$

$2$

Enter the end of interval $2$

$12$

Enter the iteration error for integral

$0\mathrm{.}000001$

The integral of function between $1$ and $2$ is $-0\mathrm{.}0454551$

Enter the variable $x$

$0\mathrm{.}3$

Enter initial width for derivative

$3$

Enter the iteration error for derivative

$0\mathrm{.}00001$

The derivative of function at $x=0\mathrm{.}3$ is $-0\mathrm{.}309528$

Enter the start of interval $1$

$-5$

Enter the end of interval $2$

$3$

Enter the iteration error for integral

$0\mathrm{.}00001$

The integral of function between $1$ and $2$ is $1\mathrm{.}28768$