computer simulation

i need a C code to solve the next question using distributed random value

A baker is trying to figure out how many dozens of bagels to bake each day. Customers order a number of dozens bagels each. Bagels sell for 8.40 TL per dozen. They cost 5.80 TL. per dozen to make. All bagels not sold at the end of the day are sold at half price to a local grocery store.

Based on a long-run simulation, how many dozen (to the negrest dozen) bagels should be baked each day for given probability distributions p(r) and g(r) rethosenting the pmf for the number of customers per day, and the number of dozens cach customer buys? You are asked to assume one of the options given below

q.

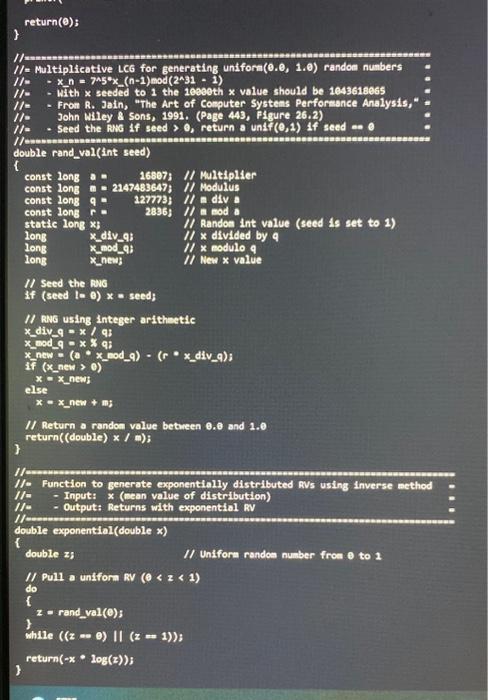
(b) p(n) and q(n) are given as p(n)={w0,10,n=11,12,,10otherwise,q(n)={55n,0.n=1,2,,10otherwise. If Return a randon value between . and 1. return ((double )/m ); 3 //o Function to generate exponentially distributed RVs using inverse eethod //= - Input: x (Gean value of distribution) I/o - Output: Returns with exponential RV double exponential(double x ) \{ double x; Unifore randon number from to 1 If Pull a uniforn RV (