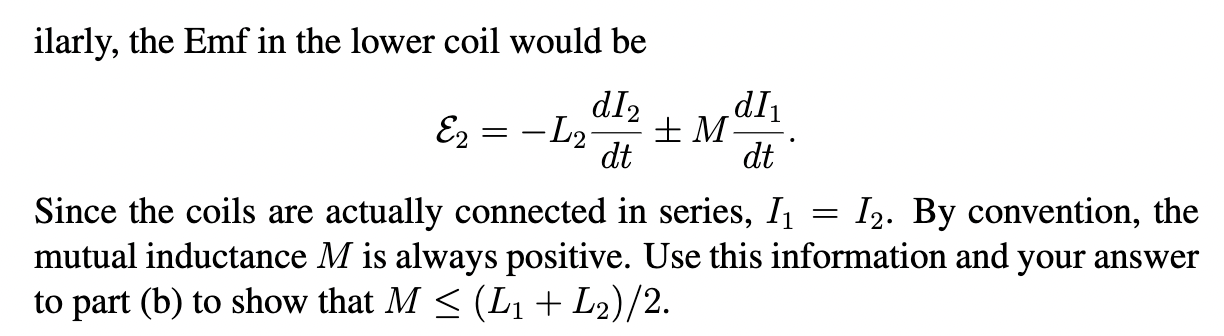
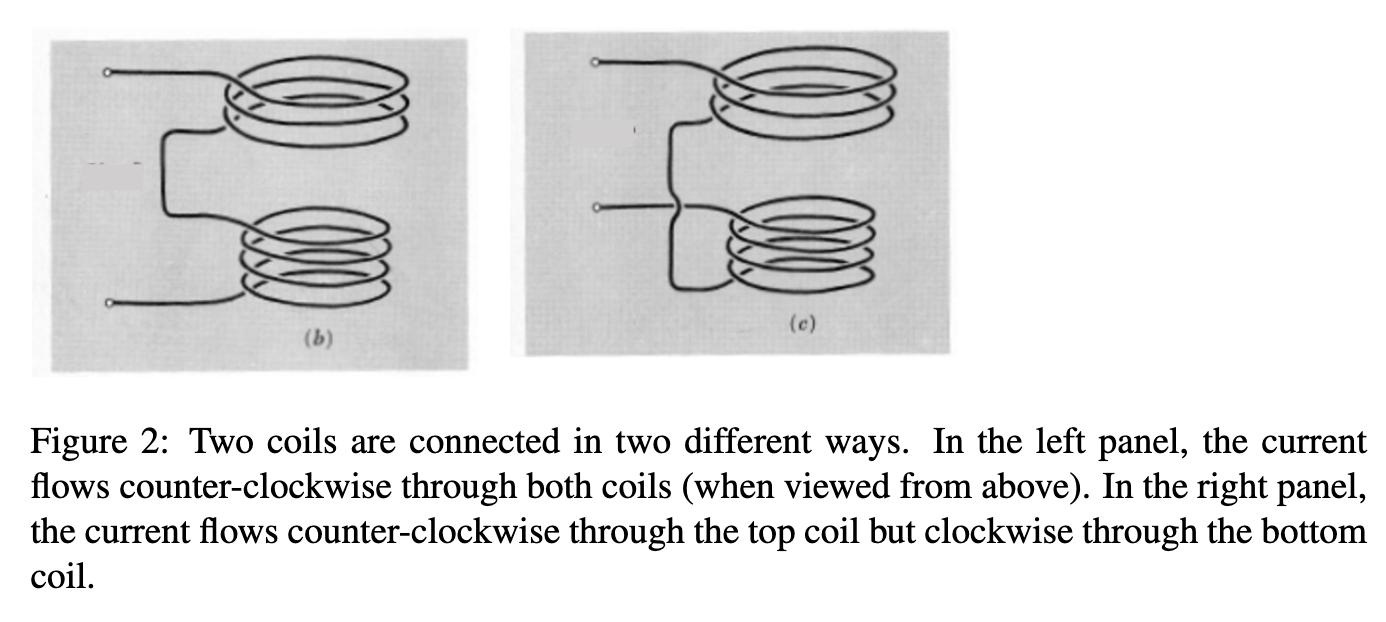
*Conceptual mutual inductance problem. Two coils are connected in series to one another in two different ways (Fig. 2). If the coils were completely separate they would have self-inductance L, and L,. If they were far away from one another but were connected 1n series, the total inductance of the circuit would be L = L + L. But, because they are actually close to each other, their mutual inductance affects the circuit. (a) Qualitatively, which circuit has the larger inductance? Why? (b) What is the smallest value possible for the total inductance of a circuit? [Hint: consider the magnetic energy.] (c) If the loops were not connected but were close to each other, the Emf in the top circuit would be dl, dl, =-L+tM & Yt dt' where [, and I, are the currents in the top and bottom coils, respectively. Sim- ilarly, the Emf in the lower coil would be d12 dl1 E2 = -L2 + M dt Since the coils are actually connected in series, I1 = 12. By convention, the mutual inductance M is always positive. Use this information and your answer to part (b) to show that M