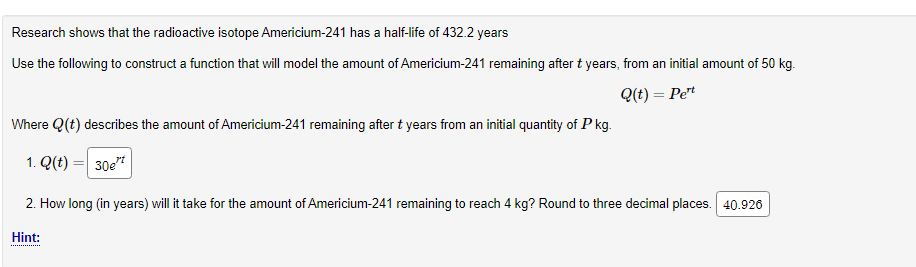
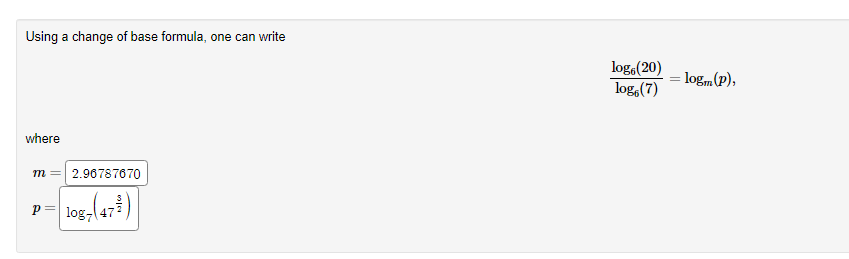
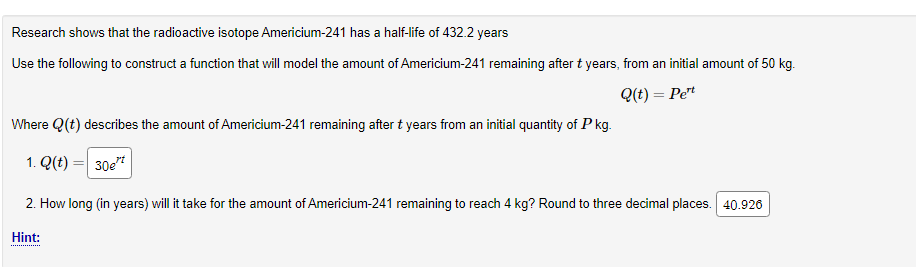
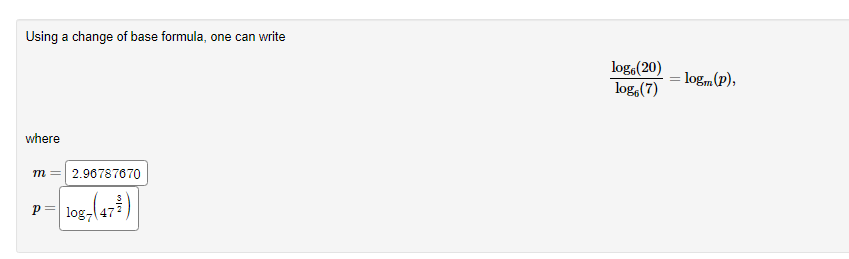
Condense the following expressions into a single logarithm by applying the properties of logarithms. . You are only allowed to use integer exponents. . Use sort(..) to deal with fractional exponents. . Make sure your final answer is written as a single logarithm. 39 a. 7log(x) + 9log(2) - , log(y) = log b. -log(x) - 9log(y) - 7log(2) = log V 9 c. - log(I) t9 / -1 -log (y) log(=) = log Hint:Exponential Growth and Decay Exponential growth and decay problems follow the model given by the equation A(t) = Pert. . The model is a function of time t . A(t) is the amount we have after time t . P is the initial amount, because for t = 0, notice how A(0) = Pelt = Pel = P . T is the growth or decay rate. It is positive for growth and negative for decay Growth and decay problems can deal with money (interest compounded continuously), bacteria growth, radioactive decay, population growth etc. So A(t) can represent any of these depending on the problem. Practice The growth of a certain bacteria population can be modeled by the function A(t) = 400e0-0572t where A(t) is the number of bacteria and t represents the time in minutes. a. What is the initial number of bacteria?| (round to the nearest whole number of bacteria.) b. What is the number of bacteria after 25 minutes?|(round to the nearest whole number of bacteria.) c. How long will it take for the number of bacteria to double? (your answer must be accurate to at least 3 decimal places.)Suppose $11000 is invested at 11% interest compounded continuously. How long will it take for the investment to grow to $22000? Use the model A(t) = Pe" and round your answer to the nearest hundredth of a year. It will take years for the investment to reach $22000.Research shows that the radioactive isotope Americium-241 has a half-life of 432.2 years Use the following to construct a function that will model the amount of Americium-241 remaining after t years, from an initial amount of 50 kg. Q(t) = Pert Where Q (t) describes the amount of Americium-241 remaining after t years from an initial quantity of P kg. 1. Q(t) 30ert 2. How long (in years) will it take for the amount of Americium-241 remaining to reach 4 kg? Round to three decimal places. 40.926 Hint: