Conditional Probability and Independence

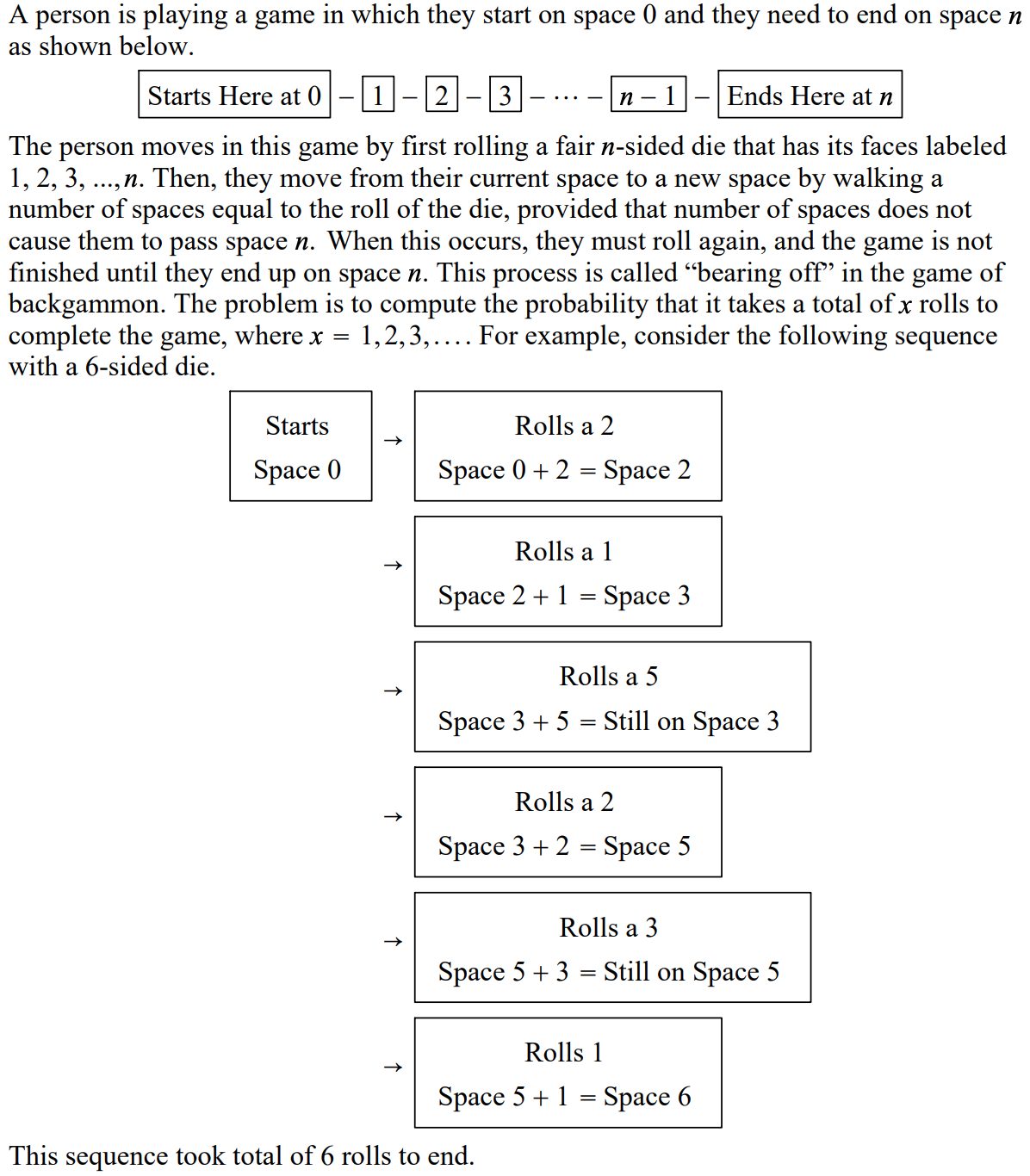
A person is playing a game in which they start on space 0 and they need to end on space It as shown below. The person moves in this game by first rolling a fair n-sided die that has its faces labeled 1, 2, 3, ...,n. Then, they move from their current space to a new space by walking a number of spaces equal to the roll of the die, provided that number of spaces does not cause them to pass space n. When this occurs, they must roll again, and the game is not nished until they end up on space 11. This process is called \"bearing off\" in the game of backgammon. The problem is to compute the probability that it takes a total of x rolls to complete the game, where x = l, 2,3,... . For example, consider the following sequence with a 6-sided die. Starts Rolls a 2 Space 0 Space 0 + 2 = Space 2 Rolls a 1 Space 2 + 1 = Space 3 Rolls 3 5 Space 3 + 5 = Still on Space 3 Rolls a 2 Space 3 + 2 = Space 5 Rolls a 3 Space 5 + 3 = Still on Space 5 Rolls 1 Space 5 + 1 = Space 6 This sequence took total of 6 rolls to end