Conducting sphere conditioner questions.

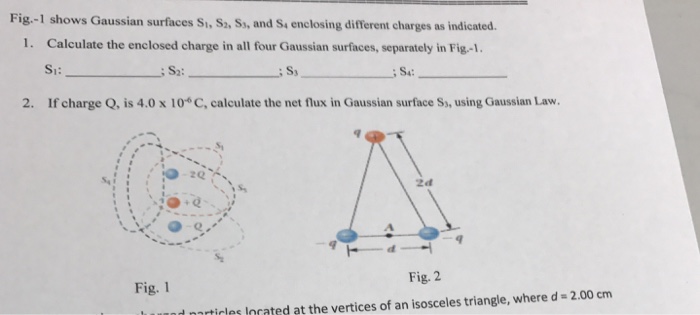
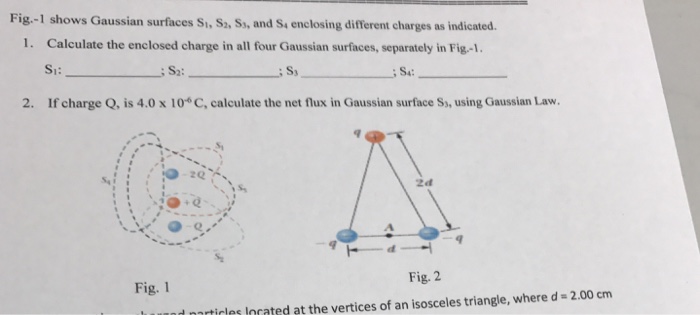
The potential inside a conducting sphere of radius R is a. directly proportional to radius "r" of the Gaussian Surface. b. Inversely proportional to the radius "r" of the Gaussian surface. C C. a constant. d. zero. O e. inversely proportional to the square of the radius "r" of the Gaussian surface. O F. infinite.(2) (a) For the charge configuration shown below, draw eight electric field lines. Then draw a Gaussian surface that encloses both positive charges. What is the net number of electric field lines exiting the Gaussian surface minus the net number entering the Gaussian surface? (b) Repeat part (a) except with a Gaussian surface that encloses just the negative charge. (c) Repeat part (a) except with a Gaussian surface that encloses all three charges. -2q + 9 + 9Fig.-1 shows Gaussian surfaces Si, Sz, Sy, and S, enclosing different charges as indicated. 1. Calculate the enclosed charge in all four Gaussian surfaces, separately in Fig.-1. SI: : S2: ; S4: 2. If charge Q, is 4.0 x 10*C, calculate the net flux in Gaussian surface S3, using Gaussian Law. 40 Fig. 2 Fig. 1 icles Inrated at the vertices of an isosceles triangle, where d = 2.00 cm