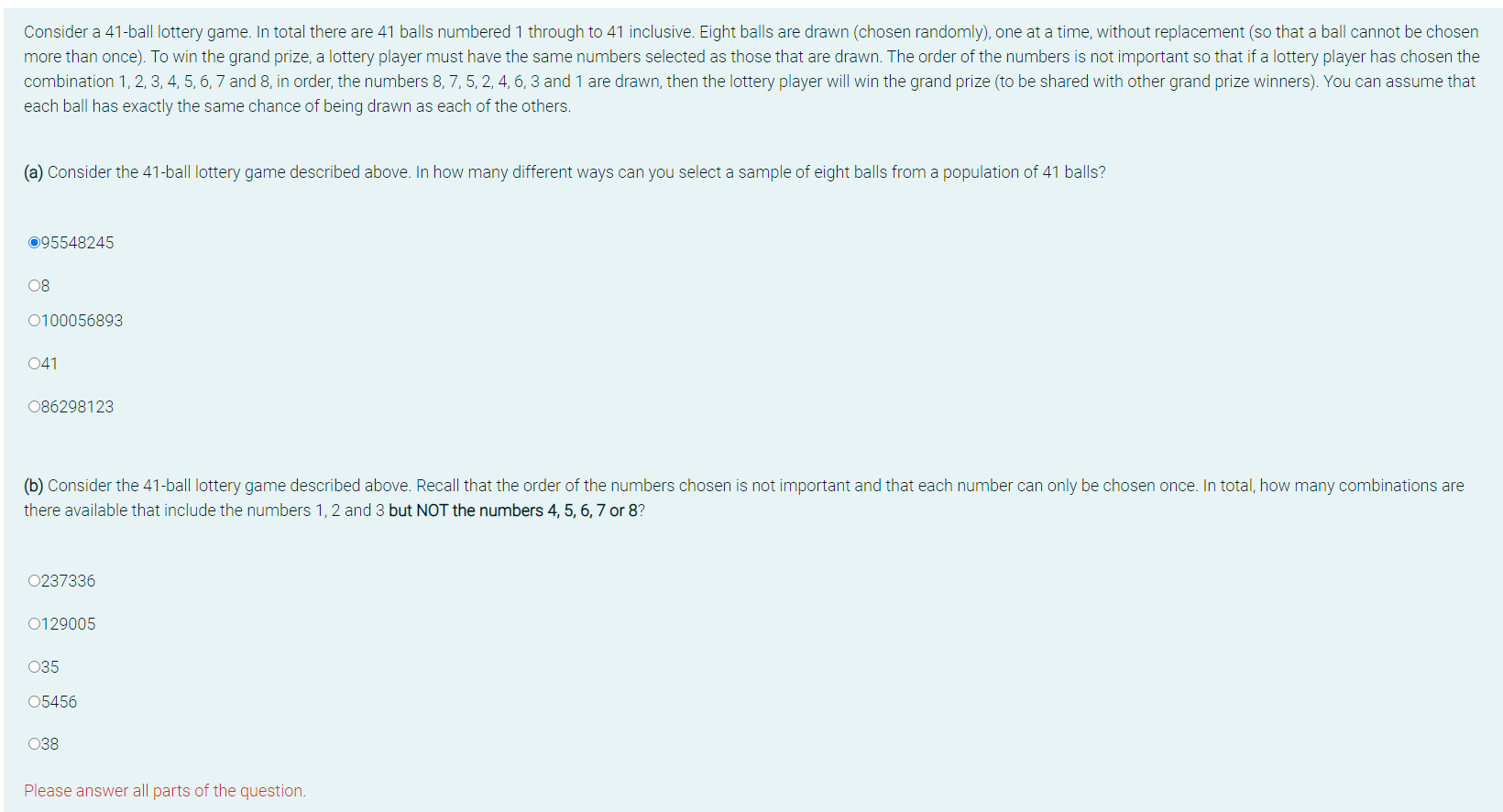
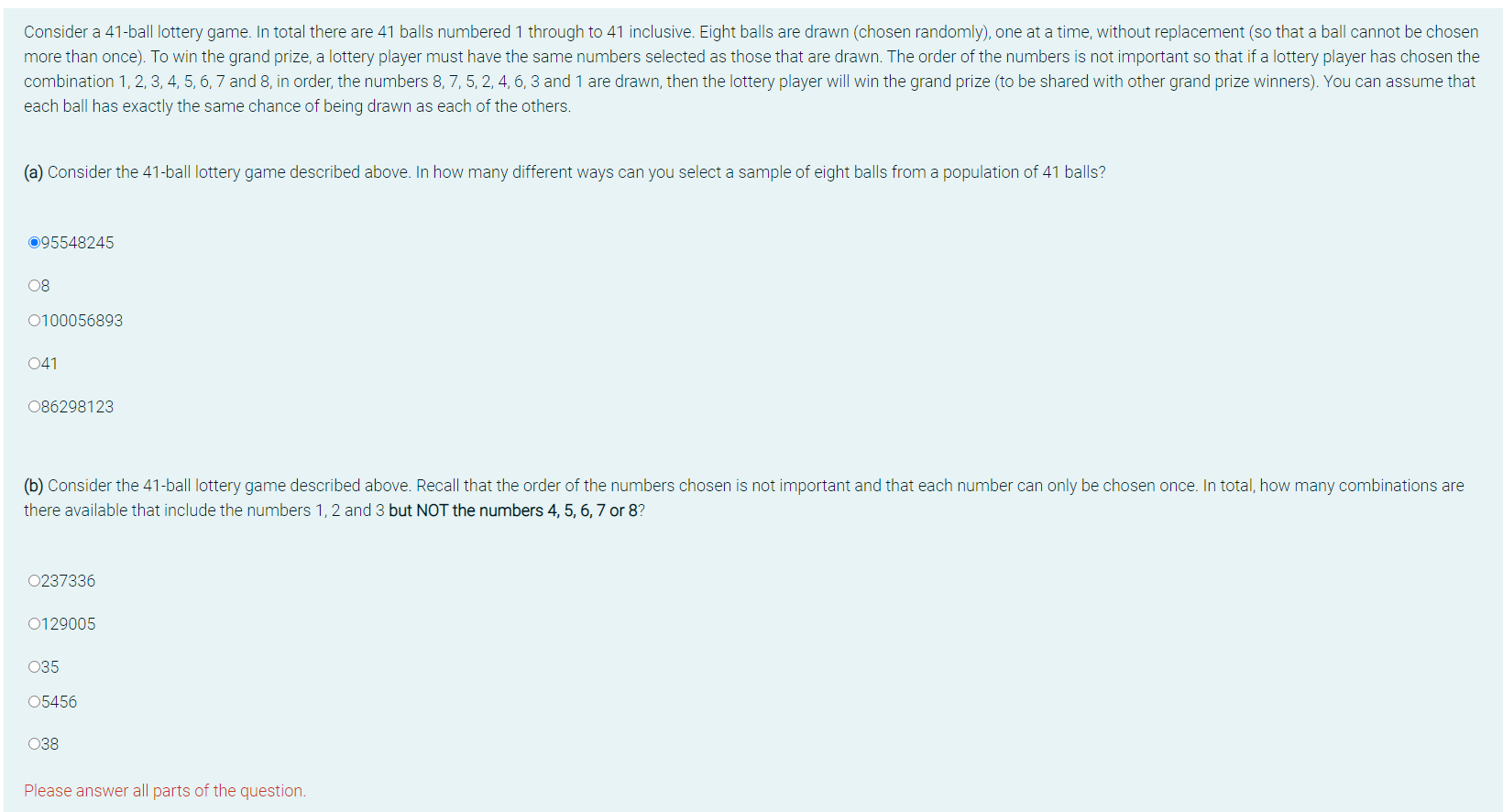
Consider a 41-ball lottery game. In total there are 41 balls numbered 1 through to 41 inclusive. Eight balls are drawn (chosen randomly), one at a time, without replacement (so that a ball cannot be chosen more than once). To win the grand prize, a lottery player must have the same numbers selected as those that are drawn. The order of the numbers is not important so that if a lottery player has chosen the combination 1, 2, 3, 4, 5, 6, 7 and 8, in order, the numbers 8, 7, 5, 2, 4, 6, 3 and 1 are drawn, then the lottery player will win the grand prize (to be shared with other grand prize winners). You can assume that each ball has exactly the same chance of being drawn as each of the others. (a) Consider the 41-ball lottery game described above. In how many different ways can you select a sample of eight balls from a population of 41 balls? 095548245 08 0100056893 041 086298123 (b) Consider the 41-ball lottery game described above. Recall that the order of the numbers chosen is not important and that each number can only be chosen once. In total, how many combinations are there available that include the numbers 1, 2 and 3 but NOT the numbers 4, 5, 6, 7 or 8? 0237336 0129005 035 05456 038 Please answer all parts of the