Consider a bivariate normal

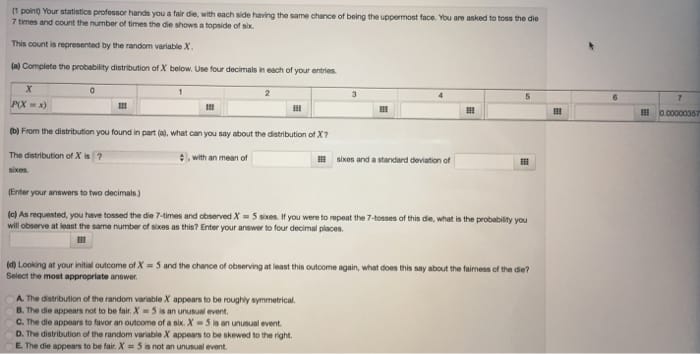
3. Suppose that O ~ Unif (0, 27) and V ~ Exp(1/8). Define X1 = VV cos and X2 = VV sin O. Let X = (X1, X2) be a bivariate random vector. (a) Find the distribution of the random vector X. (b) Find a scalar c such that Z = cX follows the standard bivariate normal distribution. (c) Find a lower triangular matrix A and a vector b such that b + AZ follows the bivariate normal distribution N(u, E), where 4 U = E = 9Consider a bivariate normal population with #1 = 0, /2 = 2, 011 = 2, 622 = 1, and P12 = 0.5. (a) Write out the bivariate normal density. (b) Write out the squared generalized distance expression (x - p)'E-1(x - ) as a function of x, and x2. (c) Determine and sketch the constant-density contour that contains 50% of the probability.Consider a bivariate normal population with #1 = 0, /2 = 2, 011 = 2, 622 = 1, and P12 = 0.5. (a) Write out the bivariate normal density. (b) Write out the squared generalized distance expression (x - p)'E-1(x - ) as a function of x, and x2. (c) Determine and sketch the constant-density contour that contains 50% of the probability.[1 point Your statisticn professor harch you a fair die. with each side haning the same chance of being the uppermost face. You are asked to toss the die T times and count the number of times the din shows a topside of his. This count is represented by the random variable X' [a) Complete the probability distribution of X' below, Use four decimals in each of your entries X 2 (b) From the distribution you found in part jai, what can you say about the datribution of X? The distribution of X is 7 : . with an mean of sixes and a standard deviation of [Enter your answers to two docimain] (o) As requested, you have tossed the die 7-times and observed ) = 5 woes if you were to repeat the 7-teases of this de, what is the probability you will observe at least the sarma number of was as this? Enter your answer to four decimal places. (d) Looking at your initial outcome of X = 3 and the chance of observing at least this outcome again, what dous this say about the faimess of the die? Select the most appropriate answer. A. The onlybution of the random variable X appears to be roughly symmetrical, B. The die appears not to be fair, J' - 3 is an unusual event, C. The die appears to favor an outcome of a six. )' - 5 in an uninual event. D. The distribution of the random varable X appar's to be skewed to the right, E. The die appears to be fait X' = 5 a not an unusual event