Question: Consider a box with dimensions 3cm x 5cm x 11cm. If all of its dimensions are increased by x cm, what values of x will

Consider a box with dimensions 3cm x 5cm x 11cm. If all of its dimensions are increased by x cm, what values of x will give a box with a volume between 300cm^3 and 900cm^3?

will give a box with a volume between 300cm^3 and 900cm^3? Solution:

Find the roots of the following cubic equation: 1x3 + 19x2 +

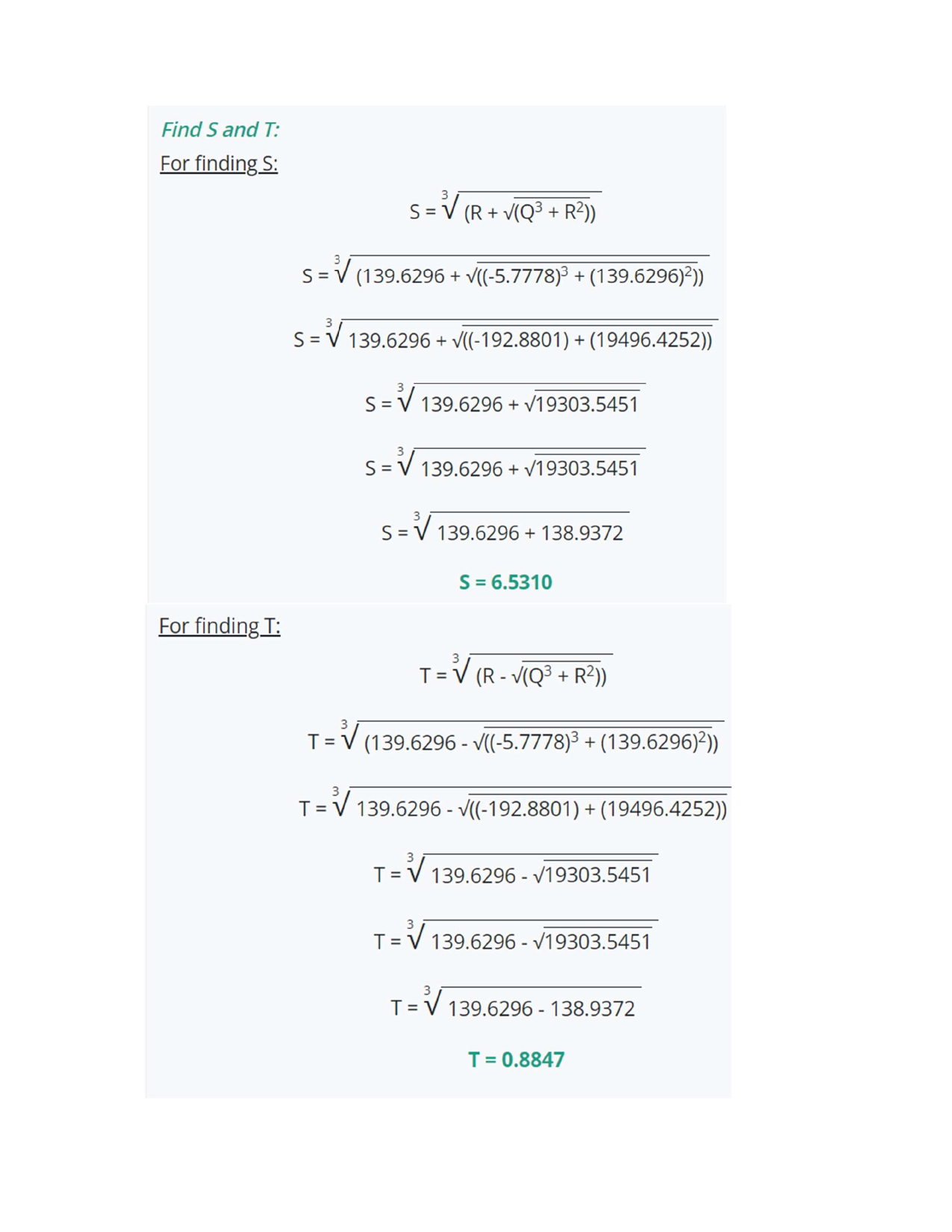
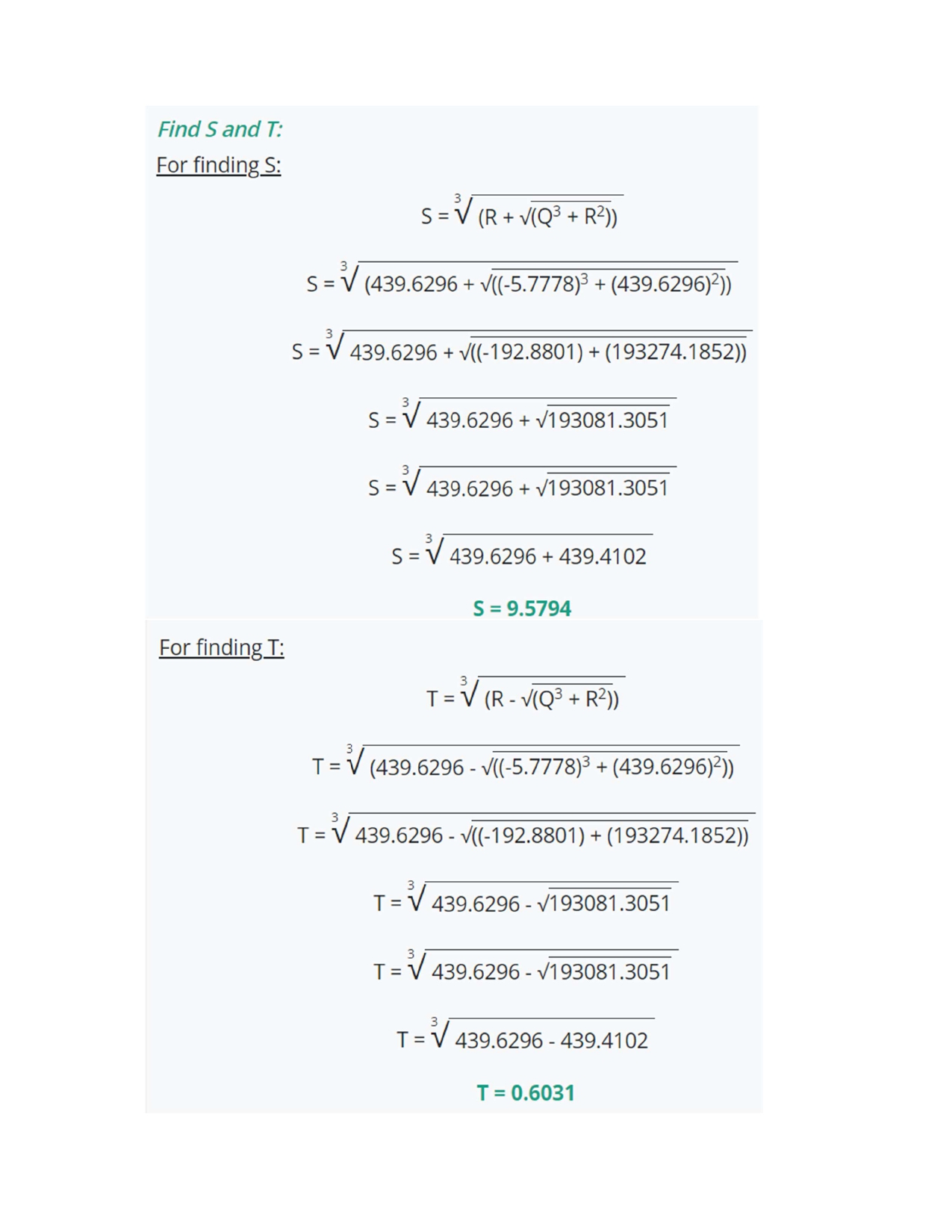
Solution: Find the roots of the following cubic equation: 1x3 + 19x2 + 103x + -135 = 0 The coefficients of cubic equation are: a = 1 , b= 19, c = 103, d = -135 Find Q and R: For finding Q: Q - 3ac - 62 9a2 0 = (3)(1)(103) - (19)2 (9)(1)2 Q = (309) - (361) (9)(1) Q =-5.7778 For finding R: R = 9abc - 27a2d - 263 54a3 R = [(9)(1)(19)(103)] - [(27)(1)2(-135)] - [(2)(19)] (54)(1) 3 R= (17613) - (-3645) - (13718) 54 R = ! 7540 54 R = 139.6296Find S and T: For finding S: S = V(R + V(Q3 + R2)) S = V (139.6296 + V((-5.7778)3 + (139.6296)2)) S = V 139.6296 + V((-192.8801) + (19496.4252)) S = V 139.6296 + V19303.5451 S = V 139.6296 + V19303.5451 S = V 139.6296 + 138.9372 S = 6.5310 For finding T: T= V (R - V(Q3 + R2)) T= V (139.6296 - V((-5.7778)3 + (139.6296)2)) T = V 139.6296 - V((-192.8801) + (19496.4252)) T = V 139.6296 - 19303.5451 T = V 139.6296 - V19303.5451 T = V 139.6296 - 138.9372 T = 0.8847Finally Use the roots formula: First root (X1): X1 = S+ T - b/3a X1 = 6.5310 + 0.8847 - 19/(3)(1) X1 = 6.53100.8847 - 19/3 X1 = 1.0824 Second root (X2): X2 = -(S+ T)/2 + (S- T)* iV3/2 - b/3a X2 = -((6.5310) + (0.8847))/2 + ((6.5310) - (0.8847))* iV3/2 - (19)/(3)(1) X2 = -(6.53100.8847)/2 + (5.6463)* (0.867)i - (19)/(3) X2 = -(6.53100.8847)/2 + (5.6463)* (0.867)i - (19)/(3) X2 = -(3.7078) - (6.3333) + (5.6463) * (0.867)i X2 =-10.0412 + 4.8953i Third root (X3); X3 = -(S + T)/2 - (S- T)*iv3/2 - b/3a X3 = -((6.5310) + (0.8847))/2 - ((6.5310) - (0.8847))* iv3/2 - (19)/(3)(1) X3 = -(6.53100.8847)/2 - (5.6463)* (0.867)i - (19)/(3) X3 = -(6.53100.8847)/2 - (5.6463)* (0.867)i - (19)/(3) X3 = -(3.7078) - (6.3333) - (5.6463) * (0.867)i X3 =-10.0412 - 4.8953iSolution: Find the roots of the following cubic equation: 1x3+19x%2 +103x +-735=0 The coefficients of cubic equation are: a=1,b=19,=103,d=-735 Find Q and R: For finding Q: 3ac - b? 9a? _(3)(1)(103) - (19)* (9)(1)? (309) - (361) (9)(1) Q=-5.7778 Q: Q: For finding R: _9abc - 27a%d - 2b 54a3 R = [(9)(1)(19)(103)] - [(27)(1)*(-735)] - [(2)(19)] (54)(1) R = (17613) - (-19845) - (13718) 54 R = 23740 54 R =439.6296 R \fFinally Use the roots formula: First root (X1.): X1 = S + T - b/3a X1 = 9.5794 + 0.6031 - 19/(3)(1) X1 = 9.57940.6031 - 19/3 X1 = 3.8492 Second root (X2): X2 = -(S + T)/2+ (S- T)*iV3/2 - b/3a X2 = -((9.5794) + (0.6031))/2 + ((9.5794) - (0.6031))* iV3/2 - (19)/(3)(1) X2 = -(9.57940.6031)/2 + (8.9763)* (0.867)i - (19)/(3) X2 = -(9.57940.6031)/2 + (8.9763)* (0.867)i - (19)/(3) X2 = -(5.0912) - (6.3333) + (8.9763) * (0.867)i X2 =-11.4246 + 7.7825i Third root (X3): X3 = -(S + T)/2 - (S- T)* iV3/2 - b/3a X3 = -((9.5794) + (0.6031))/2 - ((9.5794) - (0.6031))* iV3/2 - (19)/(3)(1) X3 =-(9.57940.6031)/2 - (8.9763)* (0.867)i - (19)/(3) X3 = -(9.57940.6031)/2 - (8.9763)* (0.867)i - (19)/(3) X3 = -(5.0912) - (6.3333) - (8.9763) * (0.867)i X3 =-11.4246 - 7.7825i

Step by Step Solution

There are 3 Steps involved in it

1 Expert Approved Answer

Step: 1 Unlock blur-text-image

Question Has Been Solved by an Expert!

Get step-by-step solutions from verified subject matter experts

Step: 2 Unlock

Step: 3 Unlock

Students Have Also Explored These Related Mathematics Questions!

Fowlkes et al. (1988) reported results of a survey of employees of a large national corporation to determine how satisfaction depends on race, gender, age, and regional location. The data are at the...

Hello, I was wondering if you could help me with two questions I am stuck on. The first question is: 1.The dimensions of a box are 3cm x 5cm x 7cm. The width, length, and height of the box must be...

Unit 1 Assignment 1. Rod says that he is thinking of a one variable polynomial expression that has the following characteristics: a. has a degree of 4 b. has three terms c. one of the terms has...

1. Rod says that he is thinking of a one variable polynomial expression that has the following characteristics: a. has a degree of 4 b. has three terms c. one of the terms has degree 1 d. one of the...

15. Consider a box with dimensions 3 cm x 5 cm x 11 cm. If all of its dimensions are increased by x cm, what values of x will give a box with a volume between 300 cm3 and 900 CW? [6 marks]

Solve the inequality (2)/(3) (2+5)(97). Include an interval chart in your solution. 14. Solve the inequality 8 3 2 + 1 17 8. Explain your solution in words. 15. Consider a box with dimensions 3 cm 5...

Consider a box with dimensions 3 cm 5 cm 1 1 cm . If all of its dimensions are increased by x cm , what values of x will give a box with a volume between 3 0 0 cm 3 and 9 0 0 cm 3 ? [ 6 marks ]

Consider a box with dimensions of 3cmx5cmx11cm. If all of it's dimensions are increased by x cm, what values of x will give a box with a volume between 300 cm^3 and 900cm^3

Consider a uniformly charged, perfectly spherical bowling ball of radius 1 5 cm centered at some origin and carrying a charge density of 3 5 uC / m 3 . a . What would be the flux through a closed,...

Math\t107-6381\t-\tQuiz\t#4\t-\tSchultz\t-\tDue\tFebruary\t21,\t2016\t-\tpage\t1\tof 3 Follow\tthese\tdirections\tcarefully. This\tquiz\tis\tdue\tby\t11:59\tEastern\ttime\ton\tFebruary\t21,\t2016. o...

Do you think Revolights will need to raise additional capital? If so, why? Using Table 10.2 in the chapter as a guide, if Revolights raises additional capital, what would be the most appropriate...

You are comparing the regression output across two publicly-traded companies. Both regressions were run using monthly data for 5 years and against the S&P500 with the returns on each companys...

E5.18 A system is shown in Figure E5.18(a). The response to a unit step, when K = 1, is shown in Figure E5.18(b). Determine the value of K so that the steadystate error is equal to zero. 1.0 0.8 y(t)...

SecuriCorp operates a fleet of armored cars that make scheduled pickups and deliveries in the Los Angeles area. The company is implementing an activity-based costing system that has four activity...