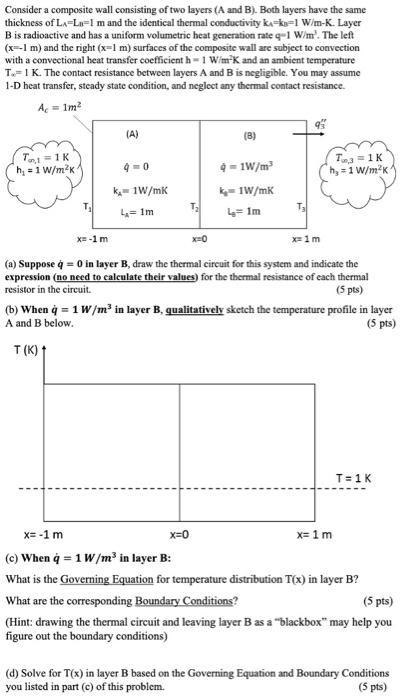
Consider a composite wall consisting of two layers (A and B). Both layers have the same thickness of LA-La-1 m and the identical thermal conductivity ka-ka-1 W/m-K. Layer B is radioactive and has a uniform volumetric heat generation rate q-1 W/m. The left (x=-1 m) and the right (x-1 m) surfaces of the composite wall are subject to convection with a convectional heat transfer coefficient h-1 W/mK and an ambient temperature T.= 1 K. The contact resistance between layers A and B is negligible. You may assume 1-D heat transfer, steady state condition, and neglect any thermal contact resistance. A = 1m T1=1 K h, 1 W/mK/ T (A) x= -1 m 9=0 k= 1W/mK L=1m T x=0 (8) 9-1W/m k=1W/mK 4= 1m x=0 T xem (a) Suppose q = 0 in layer B, draw the thermal circuit for this system and indicate the expression (no need to calculate their values) for the thermal resistance of each thermal resistor in the circuit. (5 pts) T = 1 K h, 1 W/mKA (b) When q = 1 W/m in layer B, qualitatively sketch the temperature profile in layer A and B below. (5 pts) T(K) x= -1 m (c) When q = 1 W/m in layer B: What is the Governing Equation for temperature distribution T(x) in layer B? What are the corresponding Boundary Conditions? x= 1 m T= 1 K (5 pts) (Hint: drawing the thermal circuit and leaving layer B as a "blackbox" may help you figure out the boundary conditions) (d) Solve for T(x) in layer B based on the Governing Equation and Boundary Conditions you listed in part (c) of this problem. (5 pts)