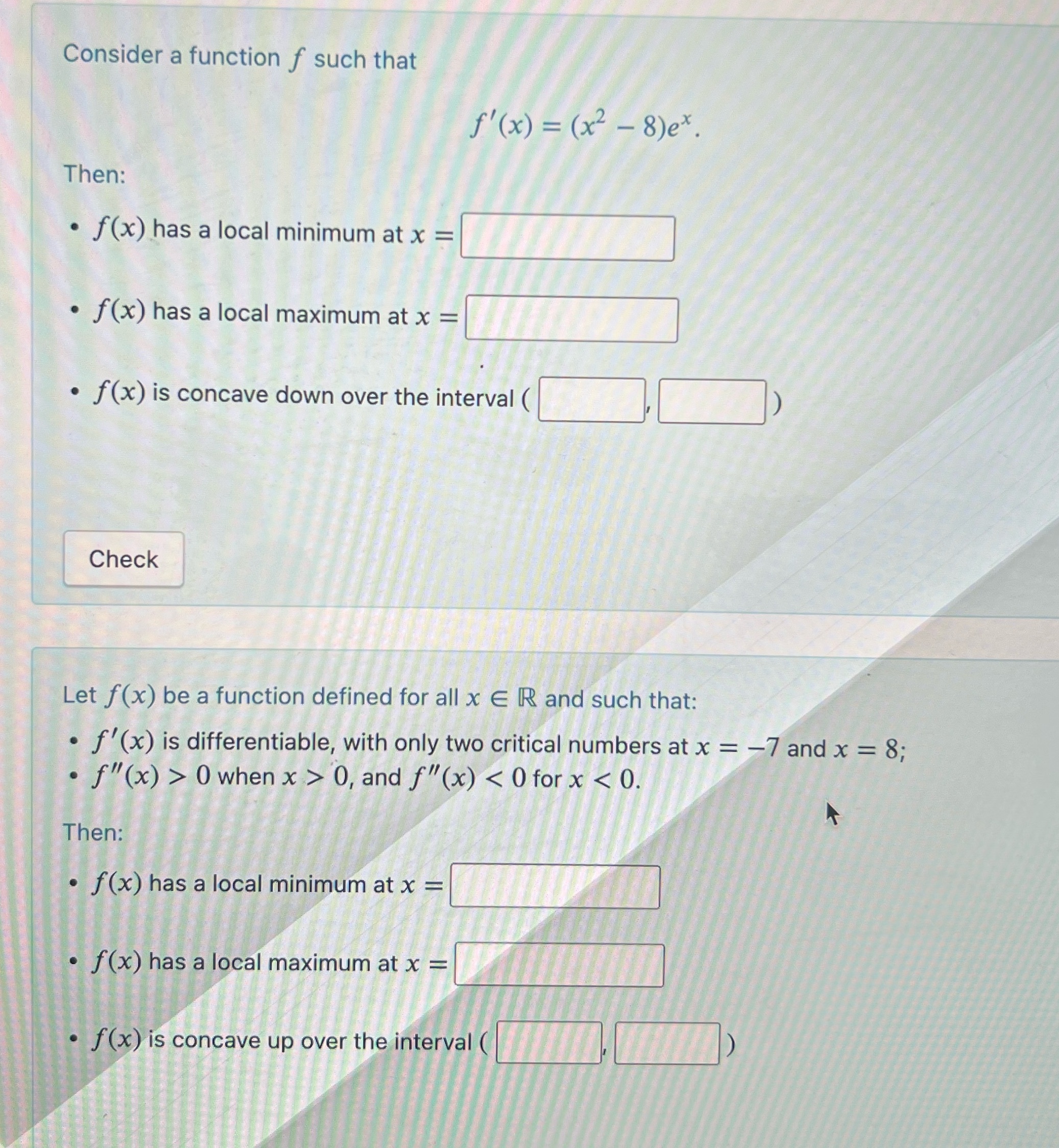
Consider a function f such that f' (x) = (x2 - 8)ex. Then: . f (x) has a local minimum at x = . f (x) has a local maximum at x = . f(x) is concave down over the interval ( Check Let f(x) be a function defined for all x E R and such that: . f' (x) is differentiable, with only two critical numbers at x = -7 and x = 8; . f"(x) > 0 when x > 0, and f"(x)