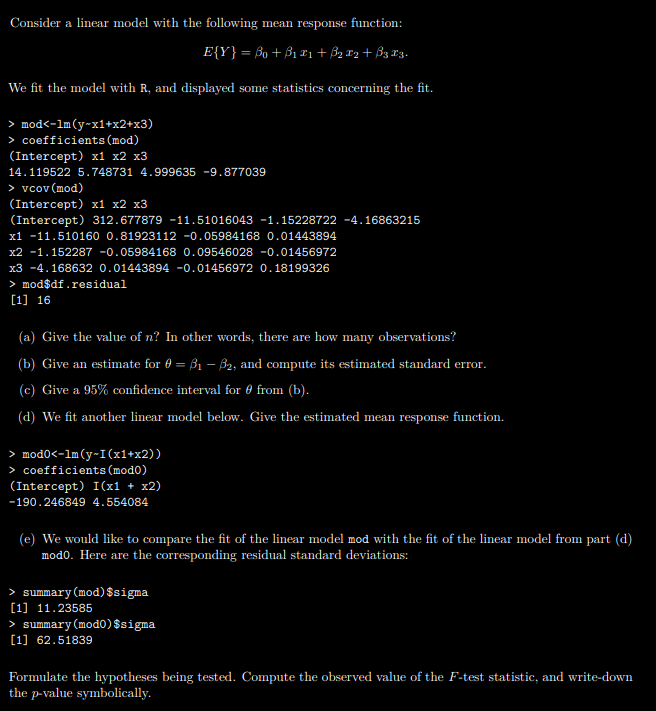
Consider a linear model with the following mean response function: E(Y ) = Bo + Pix1 + 82 12 + B3 13. We fit the model with R, and displayed some statistics concerning the fit. mod vcov (mod) (Intercept) x1 x2 x3 (Intercept) 312.677879 -11.51016043 -1. 15228722 -4. 16863215 x1 -11 . 510160 0.81923112 -0. 05984168 0. 01443894 x2 -1. 152287 -0. 05984168 0. 09546028 -0.01456972 x3 -4. 168632 0. 01443894 -0. 01456972 0. 18199326 > mod$df . residual [1] 16 (a) Give the value of n? In other words, there are how many observations? (b) Give an estimate for 6 = 81 - 82, and compute its estimated standard error. (c) Give a 95% confidence interval for @ from (b). (d) We fit another linear model below. Give the estimated mean response function. mod0 coefficients (modo) (Intercept) I(x1 + x2) -190. 246849 4. 554084 (e) We would like to compare the fit of the linear model mod with the fit of the linear model from part (d) mod0. Here are the corresponding residual standard deviations: summary (mod) $sigma [1] 11.23585 > summary (modO) $sigma [1] 62.51839 Formulate the hypotheses being tested. Compute the observed value of the F-test statistic, and write-down the p-value symbolically