Consider a minimum cost network flow problem instance with five nodes. Suppose node 1 has a supply of 32 units, node 4 has a demand of 22 units and node 5 has a demand of 10 units. The remaining nodes (nodes 2 and 3) are transshipment nodes. The arcs of the network with their capacities and unit cost values are provided in the below table.

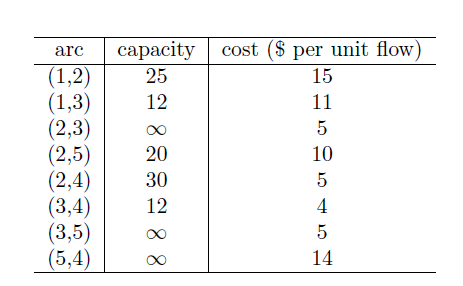
Solve the problem using network simplex. Start with the feasible basic solution x12 = 20, x25 = 10, x34 = 12, x24 = 10, (x13 = 12).

\begin{tabular}{c|c|c} \hline arc & capacity & cost (\$ per unit flow) \\ \hline(1,2) & 25 & 15 \\ (1,3) & 12 & 11 \\ (2,3) & & 5 \\ (2,5) & 20 & 10 \\ (2,4) & 30 & 5 \\ (3,4) & 12 & 4 \\ (3,5) & & 5 \\ (5,4) & & 14 \\ \hline \end{tabular}