1. Consider a multiple regression model of your choice containing two predictors. Calculate the values of the regression equation with a range chosen by you for the values of the predictors. Provide the graph of the regression equation which is a plane.
2. Augment your regression model by a sigmoid posterior filter. Calculate the values of the regression equation within the range chosen in part 1. Provide the graph of the regression equation, which will be a sigmoidal surface. Show that this graph cannot have a local extremum.
3. Now, add another regression model with sigmoid posterior containing the same two predictors in the previous part. Repeat parts 1 and 2 for this new regression model.
4. Now consider a neural net model, which has two parallel hidden layers, which are the two regression models considered above. The output of the net is simply the superposition of the two regression models. Show that by proper choice of the parameters you can have an output, which has a local extremum within the choice for the range of the values of the predictor. Provide the graph of the regression equation.
5. How does this observation indicate an application of neural networks modeling in practice?

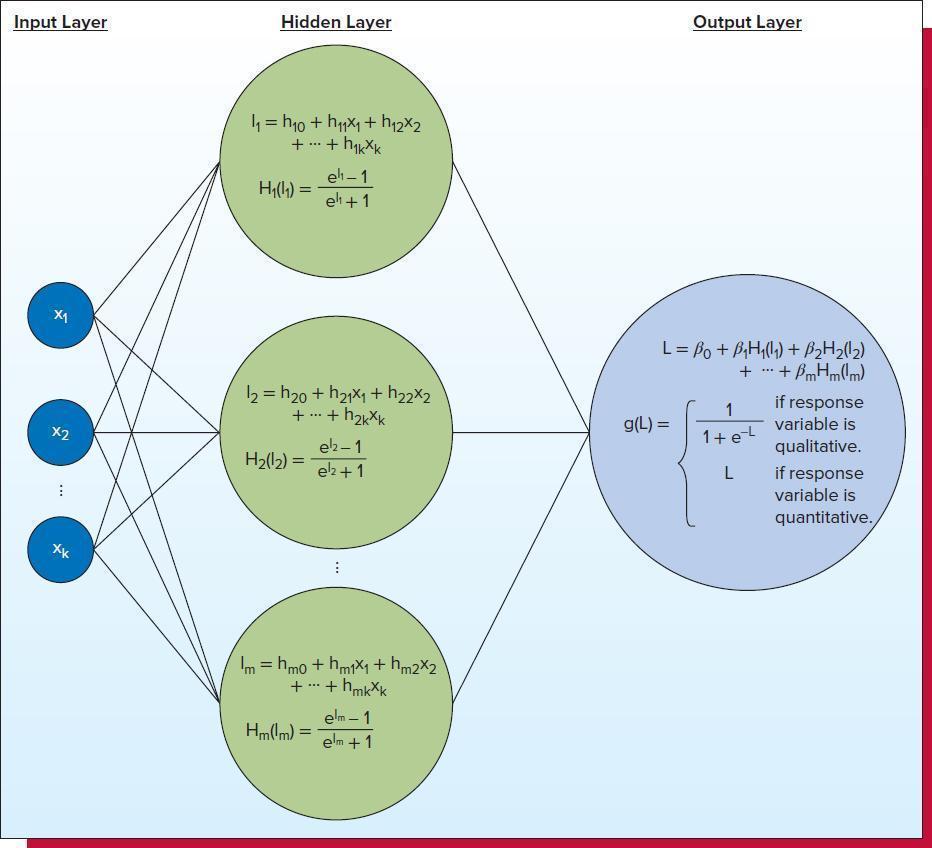
Input Layer Hidden Layer Output Layer 1, = h10 + hux + h12*2 + ... + hikXk Hi ( 1 1 ) = e ell - 1 ell + 1 L = Bo + ByH1(19) + B2H2(12) + + /mHm (m) 12 = h20+ h21x, + h22x2 if response + .+ hzkxk X2 g(L) = 1tel variable is H2 (1 2 ) = e/2- 1 qualitative. e2 + 1 L if response variable is quantitative. XK Im = hmo + hmix, + hm2x2 + . + hmkXk Hm(lm) = elm - 1 elm + 1Input Layer Hidden Layer Output Layer 1, = h10 + hux + h12*2 + ... + hikXk Hi ( 1 1 ) = e ell - 1 ell + 1 L = Bo + ByH1(19) + B2H2(12) + + /mHm (m) 12 = h20+ h21x, + h22x2 if response + .+ hzkxk X2 g(L) = 1tel variable is H2 (1 2 ) = e/2- 1 qualitative. e2 + 1 L if response variable is quantitative. XK Im = hmo + hmix, + hm2x2 + . + hmkXk Hm(lm) = elm - 1 elm + 1