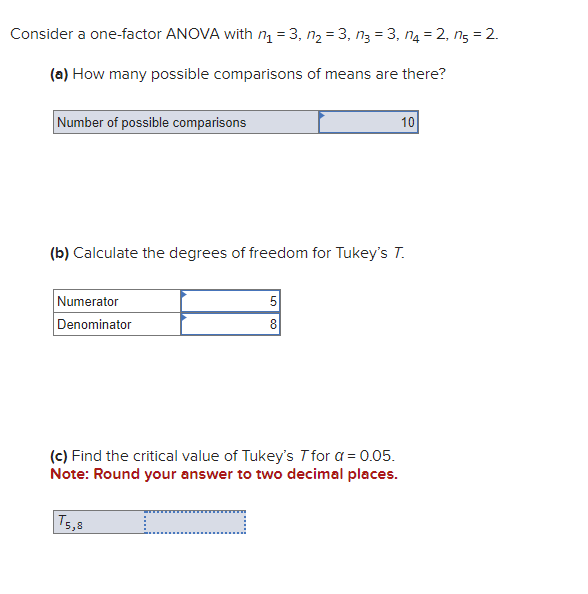
Question: Consider a one-factor ANOVA with n1 = 3, n2 = 3, n3 = 3, n4 = 2, n5 = 2. (a) How many possible comparisons
Consider a one-factor ANOVA with n1 = 3, n2 = 3, n3 = 3, n4 = 2, n5 = 2. (a) How many possible comparisons of means are there? (b) Calculate the degrees of freedom for Tukey's T. (c) Find the critical value of Tukey's T for ? = 0.05. Note: Round your answer to two decimal places.
Step by Step Solution
There are 3 Steps involved in it

Get step-by-step solutions from verified subject matter experts


