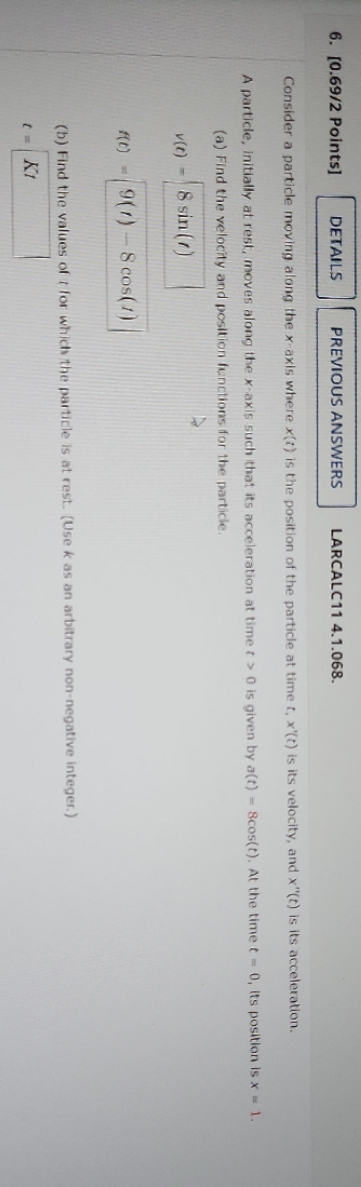
Consider a particle moving along the x-axis where x(t) is the position of the particle at time t, x'(t) is its velocity, and x"(t) is its acceleration. A particle, initially at rest, moves along the x-axis such that its acceleration at time t > 0 is given by a(t) = 8cos(t). At the time t= 0, its position is x = 1. (a) Find the velocity and position functions for the particle. v(t)=f(t) = (b) Find the values of t for which the particle is at rest. (Use k as an arbitrary non-negative integer.) t=

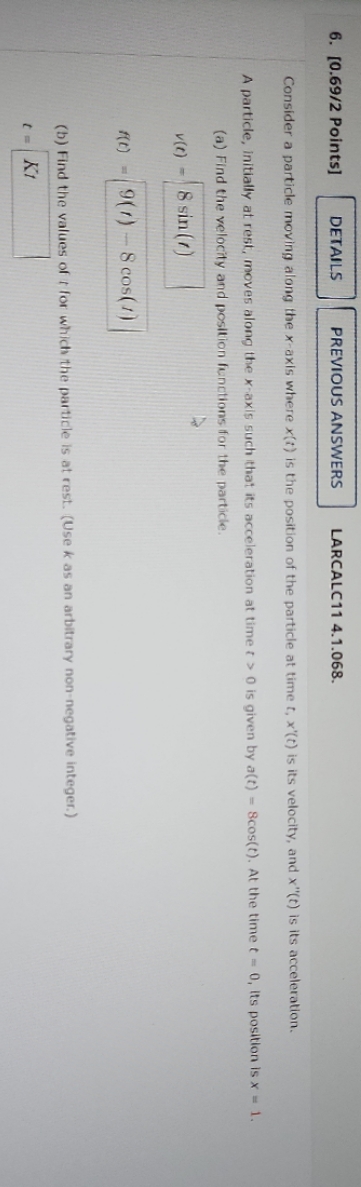
6. [0.69/2 Points] DETAILS PREVIOUS ANSWERS LARCALC11 4.1.068. Consider a particle moving along the x-axis where x(t) is the position of the particle at time t, x'(t) is its velocity, and x"(t) is its acceleration. A particle, Initially at rest, moves along the x-axis such that its acceleration at time ( > 0 is given by a(t) = Scos(t). At the time t = 0, Its position Is x = 1. (a) Find the velocity and position functions for the particle. v(( ) - 8 sin (r ) 9(1) - 8 cos( /) (b) Find the values of t for which the particle is at rest. (Use k as an arbitrary non-negative integer.)