Consider a priority queue that supports INSERT and EXTRACT-MAX operations. Given a sequence S of these operations on a set of keys {1....n}, we would like to record the sequence of extracted elements from the priority queue, storing them in an array extracted. The entire operation sequence may be processed in advance before reporting the extracted sequence.

a) In the following operation sequence S, each value i represents INSERT(i) and each `E' represents an EXTRACT-MAX call:

S = 7, 1, E, 3, 9, E, E, 2, E, E, 4, 8, E, 5, 6 Give the correct values in the extracted array.

b) To develop an algorithm for this problem, we break S into homogeneous operation subsequences:

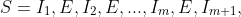where each `E' is a single EXTRACT-MAX call and each 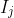represents a (possibly empty) sequence of INSERT calls. For each 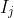, we initially place the keys inserted by that subsequence of operations into a set 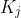, which is empty if 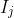is empty. We then have the following algorithm: PRIORITY-QUEUE-EXTRACTIONS(m, n) 1. for i = n downto 1 do 2. Determine j such that 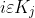3. if j 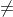m + 1 then 4. extracted[j] = i 5. Let l be the smallest value greater than j for which 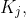exists 6. 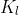= 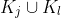, destroying 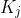7. return extracted

Argue that the array extracted returned by PRIORITY-QUEUE-EXTRACTIONS is correct.

c) Describe how to implement PRIORITY-QUEUE-EXTRACTIONS efficiently with a disjoint set data structure. d) Give a tight bound on the worst-case running time of your implementation.