Consider a quantum harmonic oscillator system, with the one-dimensional wave function n(x) where n denotes the state of the system. The ground state wave function

Consider a quantum harmonic oscillator system, with the one-dimensional wave function ψn(x) where n denotes the state of the system. The ground state wave function n = 0 and the first excited state n = 1 is given by: 

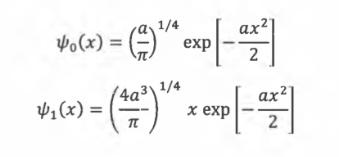
a) State the equation for the energy levels of a quantum harmonic oscillator and the energy of the first two quantum levels.

b) All wave functions of a quantum harmonic oscillator have a common exponential factor. State the exponential factor and with it, solve for a. 

c) Sketch the simple harmonic oscillator potential and the first two wave functions of the system. 

d) For a normalized arbitrary wave function y, what is the probability density function? 

e) At what location is a particle least likely to be found when in the ground state of a quantum harmonic oscillator system? How about when the system is in the first excited state?

f) A function f(x) is considered an odd function if f(-x) = -f(x) and the integration of odd functions over a symmetric interval e.g. from - b -- +b is zero. With that, calculate the expectation value of x for the ground state (x) and the first excited state (x),