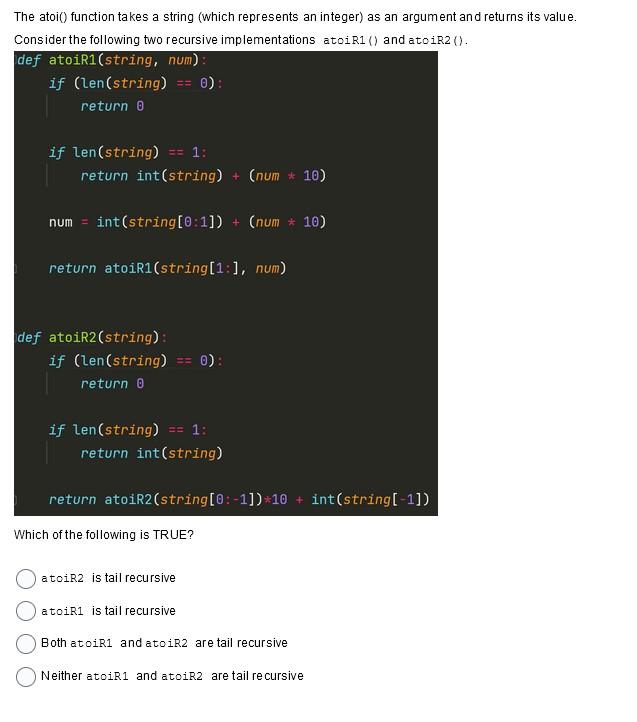
Consider a recursive function de cToBin (decimal) that converts a decimal number to a binary representation but still in base 10 . Note that all inputs and output are 32 -bit integers. Example outputs: decToBin (7)=111 (one hundred and eleven) decToBin (23)=10111 (ten thousand, one hundred and eleven) decToBin (18)=10010 (ten thousand and ten) Which one of these is a valid recursive step to the function decT oBin? None of the other answers are correct return 10 decToBin (decimal//2) + decimal//2 return decimal * 2+2decToBin(decima1/10) return 10decToBin(decimal2 ) return 10 * decToBin(decimal//2) + decimal o 2 The atoi() function takes a string (which represents an integer) as an argument and returns its value. Consider the following two recursive implementations atoiR1 () and atoiR2 }. def atoiR1 (string, num): Which of the following is TRUE? atoiR2 is tail recursive atoiR1 is tail recursive Both atoiR1 and atoiR2 are tail recursive Neither atoiR1 and atoiR2 are tail re cursive