Question: Consider a single-stage binary tree, assuming S0=4, u=2, d=1/2, r=1/4, then S1(u)=8, S1(d)=2. Suppose the strike price of the European put option is K =

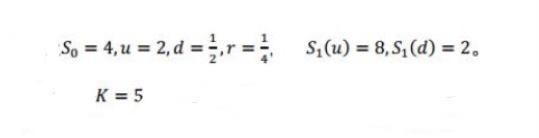

S0=4,u=2,d=21,r=41 S1(u)=8,S1(d)=2 K=5 ? S0=4,u=2,d=21,r=41,S1(u)=8,S1(d)=2 K=5 Consider a single-stage binary tree, assuming S0=4,u=2,d=1/2,r=1/4, then S1(u)=8,S1(d)=2. Suppose the strike price of the European put option is K=5. How many units of cash do investors need to prepare at the beginning of the period in order to replicate the option? Please verify your conclusions with three methods (No Arbitrage, Risk Neutral, State Price). S0=4,u=2,d=21,r=41,S1(u)=8,S1(d)=2K=5 S0=4,u=2,d=21,r=41 S1(u)=8,S1(d)=2 K=5 ? S0=4,u=2,d=21,r=41,S1(u)=8,S1(d)=2 K=5 Consider a single-stage binary tree, assuming S0=4,u=2,d=1/2,r=1/4, then S1(u)=8,S1(d)=2. Suppose the strike price of the European put option is K=5. How many units of cash do investors need to prepare at the beginning of the period in order to replicate the option? Please verify your conclusions with three methods (No Arbitrage, Risk Neutral, State Price). S0=4,u=2,d=21,r=41,S1(u)=8,S1(d)=2K=5
Step by Step Solution
There are 3 Steps involved in it

Get step-by-step solutions from verified subject matter experts


