Question: Consider a standard random walk Sn = X ++ X, with So= 0 and independent Bernoulli increments X, X,... distributed as P(X=1)=P, P(X=-1) =

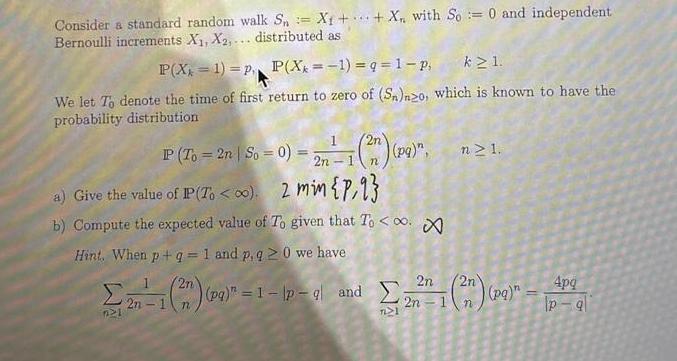
Consider a standard random walk Sn = X ++ X, with So=

Consider a standard random walk Sn = X ++ X, with So= 0 and independent Bernoulli increments X, X,... distributed as P(X=1)=P, P(X=-1) = q = 1-p, k 1. We let To denote the time of first return to zero of (Sn)n20, which is known to have the probability distribution P (To = 2n | So = 0) = 2n-1 (2) (Pq)", a) Give the value of P(To

Step by Step Solution

There are 3 Steps involved in it

1 Expert Approved Answer

Step: 1 Unlock

aEX 1PX 1 0PX 0 1p01 p p bEX 1PX 1 0PX 0 p VX EX ... View full answer

Question Has Been Solved by an Expert!

Get step-by-step solutions from verified subject matter experts

Step: 2 Unlock

Step: 3 Unlock

Students Have Also Explored These Related Accounting Questions!

Let X have a Bernoulli distribution with pmf We would like to test the null hypothesis H0: p ¤ 0.4 against the alternative hypothesis H1: p > 0.4. For the test statistic, use is a random...

Let X be a discrete random variable, with probability Distribution And P(X = x2) = ¾. (a) Determine x1 and x2, such that E(X) = 0 and variance (X) = 10. (b) Sketch the CDF of X. P(X = x,} 4 = 1

Consider Bernoulli trials with success probability p = .3. (a) Find the probability that four trials result in all failures. (b) Given that the first four trials result in all failures, what is the...

12. Consider a symmetric random walk on the integer points of the cubic lattice {(i, j, k) : i, j, k = . . . ,1, 0, 1, . . . } in three dimensions, in which the particle moves to one of its six...

EXERCISE 5.4 Consider an asymmetric random walk on a lattice with five lattice sites. Assume that the fifth site, P, absorbs the walker. The transition rates w1,2 = W1,3 = W1,4 = W1, p = , W2,1 =...

Real Cost of Hedging Payables Assume that Loras Corp. imported goods from New Zealand and needs 100,000 New Zealand dollars 180 days from now. It is trying to determine whether to hedge this...

5.9. Consider a simple random sample of size n with r respondents and m n r nonrespondents, and let yR and s2 R be the sample mean and variance of the respondents data, and yNR and s2 NR the sample...

Problem 5.2 1. Let W be a normal (Gaussian) random variable with mean 0 and variance 1. Compute the values of the moments: E{W}, E{W2}, E{W3}, E{W4}, E{W5}, E{W6}. 2. Let us now assume thatW is...

Have a C compiler which is ANSI conforming in all respects except that it has no facility for the definition, declaration or use of standard C structures. Outline a set of routines written in this...

Consider the observed frequency distribution for the following set of random variables: Random Variable, x Frequency, fo 0 17 1 35 2 30 3 15 4 and more . 3 Total 100 Perform a chisquare test...

Aslam borrowed $23 000 from Meridian Credit Union at 4% p.a. and agreed to repay the loan in monthly installments of $3000 each, such payments to cover the interest due and repayment of principal....

Joaquin goes for a job interview and is surprised that the interviewer asks him about his personal standards regarding how he would handle certain situations. He expected that the focus would be on...

Using this ER-Diagram, write an SQL Statement using CONSTRAINTS command and show atleast 1 data of the database. Write down below the SQL Statements and commands that was used. PDiagnosis PAddress...

1. (a)(i) What problem has been brought about by uncontrolled mining of minerals in Kenya? (ii) Where is fluorspar mined in Kenya? (iii) Describe how trona is mined and processed in Magadi (b) (i)...

In 2001, a commercial aircraft lost all power while flying at 10,000 m over the Atlantic Ocean, about 100 km from the Azores Islands. The skilled pilot put the plane into a gliding mode and...

Domino's Pizza franchises in New York were sued by the state of New York in 2016for wage theft at 10 stores.Under New York law, a corporation and a franchiser are joint employers if they meet certain...

Colliers, Incorporated, has 100,000 shares of noncumulative preferred stock outstanding. The preferred stock pays dividends in the amount of $2 per share, but because of cash flow problems, the...

What is the mode?

Consider a payer forward start swap where the swap begins at some fixed time Tn in the future and expires at time TM > Tn. We assume the accrual period is of length , measured in years. Since...

Consider the mean-reverting process dSt = ( St)dt + StdWt. Create a time discretization of = 1/252 and assume that the appropriate monthly model parameters are: = 0.75 = 0.35 S0 = 40 Consider the...

Let Wt be a Wiener process and t denote the time. Are the following stochastic processes martingales? (a) Xt = 2Wt + t (b) Xt = W2t (c) Xt = W2t 2 t0 sWsds

The cells in the visual cortex that respond to certain lines, edges, and angles are called _______ _______.

Depth perception underlies our ability to group similar items in a gestalt. perceive objects as having a constant shape or form. judge distances. fill in the gaps in a figure.

In listening to a concert, you attend to the star performer and perceive the other musicians as accompaniment. This illustrates the organizing principle of figure-ground. shape constancy. grouping....