Consider a triangle and a point chosen within the triangle according to the uniform probability law. Let X be the distance from the point to the base of the triangle. Given the height of the triangle, find the CDF and the PDF of X.

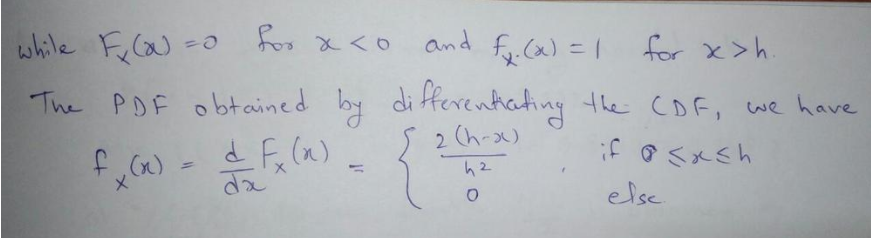
A.5 let A= bh = area of given . 2 b= length of base h= hieght of A. A - An from a random point, draw line parallel to base of let A be area of A formed. h-x = wieght of new A. b(h-x) = base of new A. hence b ( 4- x ) 2 for ac Lo,h] we have. Fy ( xx ) = 1 - P (X > x ) = 1 - Ax = 1_ b ( h-x )= = = 1_ h-x 2 A 2 h h\f