Consider a uniform rod of material whose temperature varies only along its length, in the x direction. By considering the heat flowing from both directions into a small segment of length Δx, derive the heat equation,

where K= κt/cρ, c is the specific heat of the material, and ρ is its density. (Assume that the only motion of energy is heat conduction within the rod; no energy enters or leaves along the sides.) Assuming that K is independent of temperature, show that a solution of the heat equation is

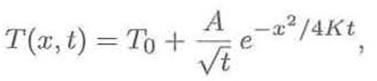
where T0 is a constant background temperature and A is any constant. Sketch (or use a computer to plot) this solution as a function of x, for several values of t. Interpret this solution physically, and discuss in some detail how energy spreads through the rod as time passes.

T = K